Img00031
35
lecz powoduje powstanie dodatkowych odmian sieci. W ten sposób powstaje 14 typów sieci, tworzących 7 głównych układów krystalograficznych (rys. 1.33-2)
35
regularny
heksagonalny
fi—
k-k
—i<P
42
r*
P--1- •
|
i tetragonalny |
1 1 | |
|
<471 |
< | |
*
romboedryczny jednoskośny
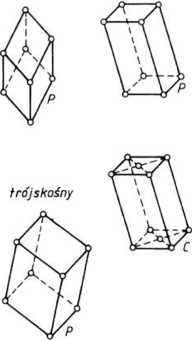
Rys. 1.33-2. Układy krystalograficzne (oznaczenia typów: P — prosty, I — przestrzennie centrowany. F — płasko centrowany, C — o centrowanej podstawie)
Tablica 1.33—1
Układy krystaliczne
|
Układ krystaliczny |
Stałe sieciowe |
Kąty w komórce elementarnej |
|
regularny |
a = b = c |
a = p = y = 90° |
|
heksagonalny |
a = b * c |
a = P = 90°, y = 120° |
|
rombowy |
a * b * c |
a = P = y - 90° |
|
romboendryczny |
a = b = c |
a = P = y * 90° |
|
jednoskośny |
a * b * c |
a = p = 90° * y |
|
tetragonalny |
a = b * c |
a = p = y = 90c |
|
trójskośny |
a* b * c |
a * p * y * 90° |
1.34. Charakterystycznymi wielkościami sieci przestrzennej określającej jej stopień zwartości jest liczba koordynacyjna i współczynnik wypełnienia.
Liczba koordynacyjna podaje liczbę atomów znajdujących się w najbliższej i równej odległości od atomu leżącego wewnątrz sieci. Na przykład w układzie regularnym prostym liczba koordynacyjna wynosi 6.
Wyszukiwarka
Podobne podstrony:
Image180 licznika, wyznaczającego kolejne adresy, powoduje oszczędność pojemności bloku pamięci. W t
57161 Obraz2�4 (3) 24 Rozdział 1 jak i odmianach gramatycznych. Ten sposób dowodzenia, zapomocą któr
skanowanie0037 (35) 40 Rozdział l. Problematyczność i prakty ka uczeń)1. W ten sposób nauczycielka s
36831 P1100093 218 Grzegorz Szpila jest w kilku odmiankach. Można i w ten sposób analizować wymienio
24 (372) g-odwrotności jakieś inne, dodatkowe warunki, definiując w ten sposób szczególne przypadki
więcej podobnych podstron