24 (372)

g-odwrotności jakieś inne, dodatkowe warunki, definiując w ten sposób szczególne przypadki g-odwrotności (na ogól jednoznacznie wyznaczalne). Czytelnik zechce zauważyć, że takim szczególnym przypadkiem jest także, omawiana wcześniej, odwrotność A"¹ (bo A A“^!A = A). W metodach opracowania wyników pomiarów szczególną role (oprócz odwrotności A"') odgrywają: g-odwrotność o minimalnej normie, g-odwrotność w metodzie najmniejszych kwadratów oraz g-odwrotność o minimalnej normie w metodzie najmniejszych kwadratów (np. Pkrelmuter 1980, Prószyński 1981, Prószyński, Sosnowski 1995, Wiśniewski 1985c, Wolf 1972, 1979).

Załóżmy, że macierz A o rzędzie r można przedstawić w następującej postaci blokowej

C

Ii

gdzie: Be9i^r-r — nieosobliwa podmacierz o rzędzie r. Wówczas jedną z g-odwrotności jest

A" =

B^_1

0

0

0

(1.23)

Możliwość takiego przedstawienia uogólnionej odwrotności A ma duże znaczenie w formułowaniu praktycznych procedur związanych z obliczaniem g-odwrotności.

Uogólniona odwrotność o minimalnej normie

Jest to taka g-odwrotność A,7_l(N) e S\^w,/‘ macierzy Ae9iⁿ'^m, że

i) A A”_(N)A = A g-odwrotność oraz dodatkowo h) (^yii(N) A) N — N A_ot^jA

gdzie: N e    - pewna macierz dodatnio określona (mówimy, że kwadrato

wa macierz B jest dodatnio określona, jeśli dla każdego wektora x ^0 zachodzi x^TB x > 0). Oznaczenia A~_(N> używamy dla odróżnienia tej odwrotności (a takie i innych dalej omawianych) od ogólnej g-odwrotności A" (dolnego indeksu m nie należy tutaj utożsamiać z wymiarem macierzy A e ).

Uogólniona odwrotność    jest taką jednoznacznie wyznaczalną

g-odwrotnością macierzy A, że

X

(1.24)

jest rozwiązaniem układu niesprzecznych równań

spełniającym własność

AX = L

X^rN X = min

(1.25)

W poprzednim podrozdziale analizowaliśmy układy równań o jednoznacznym rozwiązaniu X~A~^lL. Oznaczenia X będziemy natomiast używali w celu podkreślenia, że jest to jedno z wielu możliwych rozwiązań układu AX = L, spełniające jakieś dodatkowe kryterium, np. tutaj X⁷ N X = min. Podobne oznaczenie, nie bez powodu, będziemy również używali w dalszej części książki, mając na myśli estymatory. Wyrażenie X^;NX, nazywane też formą kwadratową, jest kwadratem normy euklidesowej wektora X względem macierzy N, co zapiszemy jako

X

N

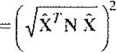
= X⁷ N X

(ijX- = yjx^rx j^st normą wektora X, natomiast jjX|j =a/X⁷ NX normą wek-

;! i! _    » >^!N

tora X względem macierzy N).

Jednym z wariantów uogólnionej odwrotności o minimalnej normie jest macierz

^A«(n) ^{= N} ‘^A' (^{A N} '^{A r})    (1-26)

Załóżmy, że Ae3i^/I"'", n < m oraz R(A) = n, skąd wynika, że istnieje odwrotność (AN"^IA⁷)"¹ macierzy AN"¹A^/ e Wówczas

A“_(N) =N“^lA^r(AN-^|A^rr¹    (1.27)

W niektórych problemach obliczeniowych mogą jednak wystąpić takie sytuacje (np. wzajemnie zależne równania warunkowe w tzw. metodzie ko-relat), że R(t\)~r<n , czyli macierz AN"¹A^ł e    jest macierzą osobliwą

o rzędzie r i defekcie d =n-r. Przyjmijmy, że macierz A można przedstawić w następującej postaci blokowej

A =

A,

A o

gdzie: A] g 9P’'", A2 £    . Zatem w macierzy A wydzielamy podmacierz A,

o wzajemnie niezależnych wierszach, przy czym liczba tych wierszy musi się równać rzędowi macierzy A. Pozostałe wiersze, w liczbie równej defektowi, tworzą podmacierz A-,. Oczywiście, tworzenie takiej struktury macierzy A