img068 (19)

dt dt dt

dt

dt

Pochodna

*0'

d Vp' dt

(f)

jest przyśpieszeniem punktu O', a pochodna

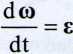
(g)

przyśpieszeniem kątowym bryły.

Występującą we wzorze (e) pochodną wektora r' względem czasu obliczyliśmy już przy wyprowadzaniu wzoru na prędkość punktu M. Jest ona dana wzorem (d). W celu obliczenia pochodnej prędkości względnej v_w względem czasu zróżniczkujemy wzór (5.81) oraz wykorzystamy zależności (5.31):

dv_w d²x'., d²y'd²z' dx'di' dy'dj' dz'dk'

dt dt²

-i +

dt²

J +

_' Ą____|

dt² dt dt dt dt dt dt

= a +-^-(o)xi') + — (cox j') + —(wxk') = ^w dt ^V ’ dt ^V ' dt ^V '

fdx'., dy'dz' /)

_=a._+ra^_₁₊__J+__kj_=aw+ro><^v.

Ch)

gdzie a_w jest przyśpieszeniem względnym punktu M:

dV., d²y'    d²z' ,

a =——1'+—'+—_rk'. ^w dt²    dt²    dt²

(5.85)

Po uwzględnieniu we wzorze (e) oznaczeń (f) i (g) oraz wzoru (h) otrzymamy przyśpieszenie a punktu M.

a = a₀, + £xr'+G>x(o)xr'+v_w) + a_w + coxv_w = = a₀, + cx r'+ ti)x (tox r')+ a_w + 2 cox v_w.

(5.86)

Pierwsze trzy wyrazy w tym wzorze znamy z ruchu ogólnego bryły jako przyśpieszenie dowolnego punktu bryły (wzór 5.33), a więc jest to przyśpieszenie unoszenia a_u:

= a₀, + £x r'+ tox (cox r').

a

(5.87)