img164

Należy wyraźnie podkreślić, że kolejne wartości x_i nie dotycząjuż wielokrotnych pomiarów tej samej wielkości przeprowadzonych w tych samych warunkach, lecz pewnego zbioru różnych jej wartości, np. różnych wartości amplitud naprężenia, przy których określamy liczbę cykli do zniszczenia.

W podobny sposób przeprowadzić można regresję liniową w przypadku zależności opisanych funkcją potęgową lub wykładniczą. W tym przypadku wyznaczenie współczynników aibz równania (6.20) poprzedzić należy wprowadzeniem nowych zmiennych w sposób opisany w punkcie 6.2.

O zgodności pomiędzy uzyskanym równaniem, a punktami pomiarowymi świadczy współczynnik korelacji liniowej r, którego wartość obliczamy ze wzoru:

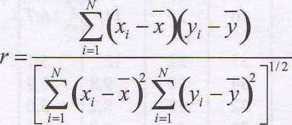
Współczynnik korelacji może przybierać wartości z zakresu -1 <r <1. Im jego wartość jest bliższa granicom wymienionego przedziału, tym lepiej prosta regresji opisuje zależność między analizowanymi zmiennymi. W szczególnym przypadku, gdyby wszystkie punkty pomiarowe leżały na prostej regresji uzyskalibyśmy pełną korelację (r = ± 1). Sytuację, w której r = -1 nazywamy czasem korelacją negatywną lub antykorelacją. Taka wartość współczynnika r świadczy o tym, że wszystkie punkty pomiarowe leżą co prawda na prostej regresji, lecz wzrostowi zmiennej niezależnej x towarzyszy spadek wartości y. Odwrotnie, o braku jakiejkolwiek korelacji między zmiennymi świadczy współczynnik korelacj i o wartości r = 0.

Analizując niewielką liczbę danych pomiarowych należy sprawdzić, czy uzyskana korelacja nie jest przypadkowa. Zauważmy bowiem, że w przypadku wykonania tylko dwóch pomiarów pewnej zależności zawsze uzyskamy r = ± 1, mimo że analizowane wielkości mogą nie być ze sobą skorelowane. Spośród kilku możliwych rozwiązań tego zagadnienia przedstawiona zostanie metoda polegająca na określeniu prawdopodobieństwa, że współczynnik korelacji mógłby być większy od z góry założonej wartości r₀ (np. otrzymanej ze wzoru (6.23)), jeśli wykonano N pomiarów nieskorelowanych ze sobą zmiennych x i y. Powyższe prawdopodobieństwa zestawiono w tablicy 6.3 [1 ]. Interpretację zamieszczonych tam wyników przedstawiono w przykładzie obliczeniowym nr 2.

97