0000032 2

4.2. Zbiory wownętrznla etabilne

Będziemy rozpatrywali podzbiory wierzchołków x'cx grafu (hipergrofu) <X,U,P> .

Podzbiorem wewnętrznie stabilny" wierzchołków grafu (hlpergrafu) joct każdy podzbiór X* tworzęcy podgraf (podhlpergraf) puaty tego grafu (hlpergrafu).

Ola grafu zapie foraalny definicji noża być następujęcy

(x'*x'*u) O P • p

Konaekwontnie, aożeay aówlć o    maksymalnych 1

naj llcżniejorych    podzbiorach wownętrznie sta

bilnych.

Liczby otebllneścl wewnętrznej «(G) grafu G nazywaay ilość wierzchołków najllczniejezego zbioru wewnętrznie atabilnego grafu C.

TY/JCROZENIE 4.3

Pbdzbiór wierzchołków X¹ grafu (hlpergrafu) G • <X,U.P>

jaot zbiorem wownętrznla fttabllnyn wtedy 1 tylko wtedy,

gdy podzbiór X \x' tworzy bazę tago grafu (hlpergrafu).

O e w ó 4 i

Załóżmy, te X¹ jaat zbloraa wewnętrznie atabllnya 1 zbiór X\x‘ nie tworzy bazy. Zatnie je wtedy galęż u CU, która nie Jeat lncydentna z żadnym x€ X\xL

Na mocy dofinlcji grafu (hlpergrafu) gałyż u muol więc być lncydentna wyłęcznle z wierzchołkami ze zbioru X¹ , a zatem X¹ nie jeet zbiorem wewnętrznie etebllnym, Uzyokana eprzeczność dowodzi prawdziwość implikacji proatej.

Załóżmy teraz. Ze zbiór X\X' tworzy bazę 1 zbiór X' nlo jeet wewnętrznie etabllny. Oznacza to, że letnie je galęż u«U lncydentna wyłęcznle z wierzchołkami ze zbioru X'. Zatem zbiór X\X^ł nie tworzy boży. Uzyokana eprzeczność kończy dowód twierdzenia.

Powyżeze twlerdzonlo dotyczy w ezczególnoścl mokoymolnych 1 najliczniejazych zbiorów wewnętrznie etabllnych oraz minimalnych i najmniej licznych baz grafu (hlpergrafu).

Wnioski i

1/    C*(G) ♦ <f(G) - |X| ;

2/ teza tnie rdzenia 4.3 noże być podstawę eetody wyznacza, nia wszystkich aakayaelnych podgrafów (podhipargrafón) pustych dowolnego grafu (hipargrafu). Metoda ta sprowadza się do wyzna, czenla wszystkich ainlaalnych baz tego grafu (hlpergrafu).

Przykład 4.1

Wyznoezyay wszystkie aaksyaalne zbiory wewnętrznie stabilne hlpergrafu z przykładu 2.1. W tya calu zauwatay, ta w przy-kładzie 3.5 wyznaczono wszystkie bazy alnlaalne tego hlpergrafu. tworzona przez podzbiory wierzchołków (i.3) » | 2.3,5.}    1 {3,4,5).

Zatea, na nocy tezy twierdzenia 4.3, aaksyaalne zbiory wownętrznie stabilna eę naetępujęcet {2,4,5} . {l.4} i {1,2}. Liczba stabilności wewnętrznoj a(H) • 3. Oczywiście tf(H) ♦ cx(M)    •

■ 2 ♦ 3 • 5 - I X |.

Przykład 4.2

Wyznaczyay wszystkie aakayaalna zbiory wewnętrznie stabilne (aakayaalne podgrafy puata) grafu z rys.2.3. W tya celu weż-aieay pod uwagę wszyatkla bezy alnlaalne tego grafu wyznaczone w przykładzie 3.6, tworzone przoz podzbiory wierzchołków {1.2.4,6.9} . (i.2.5.8.9} . jl.3,4.6.9} i {1.3.4.5.8.9} .

Na nocy twierdzenia 4.3, nakoyaalne zbiory wewnętrznie etabilne tego grofu eę naatępujęcet (3,5.7.8) , {3.4,6.7} , {2.5.7.8) i {2,6,7}. Liczba etobllnoścl wewnętrznej ^a(G) ■ 4. Ponieważ tf(G) • 5. więc tf(C) ♦ oc(C) ■ 9 • |X|.

Przykład 4.3

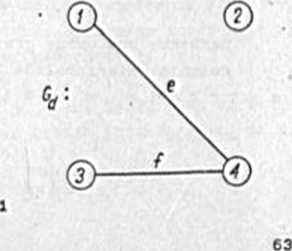
Dokonajay w klasie grafów zwykłych 0(1,0.0) pełnego prze-ględu baz, podgrafów pustych i podgrafówpołnych grafu zwykłego G 1 Jago dopełnienia G^, przadetawlonych na rya.4.1.

9«j-C»o

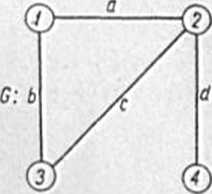
Rys.4.