Przyjmując, że wykonana ilość pomiarów pozwala założyć równość: μ = t_śr oraz σ = s_t:

6. Następnie sporządzamy tabelkę ilości k wyników pomiarów przedstawionych w tabeli w punkcie 1 przypadające na określone przedziały wielkości Δt równej 0,1 s rozłożone symetrycznie względem przedziału (tśr -0.05s, tśr +0.05s).

11,13-11,23	2
11,23-11,33	3
11,33-11,43	11
11,43-11,53	20
11,53-11,63	24
11,63-11,73	24
11,73-11,83	9
11,83-11,93	5
11,93-12,03	2

7. Teraz sporządzamy wykres (histogram) przedstawiający w postaci kolumn w poszczególnych przedziałach wyniki zawarte w tabeli w pkt. 6

III. Obliczenia:

Wartość średnia czasu wynosi

X_śr = 11,58

Następnie obliczamy odchylenie standardowe wartości średniej s­­­_tśr:

X_tśr = 0,016

Obliczamy również odchylenie standardowe pojedynczego pomiaru s_t:

S_t = 0,16

Obliczamy czas trwania jednego okresu ruchu wahadła:

T = tsr /5 =11,58/5= 2,31 [s]

Obliczamy okres wahań wahadła, traktując je jako wahadło matematyczne. Długość wahadła zmierzona od środka kulki wynosi (132.0 +/- 0,5cm)

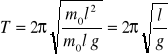
= 2,30 [s]

(∆T)_max = ±
^. ∆l

(∆T)_max = ±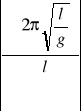
^. ∆l =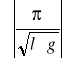
^. ∆l

(∆T)_max =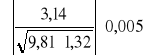
= ± 0,0044 [s]

T = 2,30 ± 0,0044 [s]

4. Wnioski:

Po przeanalizowaniu wyników doświadczenia możemy stwierdzić, ze pozornie najlepszy wynik może nie mieć żadnej wartości, jeżeli jest obarczony błędem pomiarowym. W celu zminimalizowania ilości błędów należy każdy pomiar kilkukrotnie powtórzyć, uniezależnić otrzymane pomiary od czynników zewnętrznych. Jeżeli to możliwe należy zmieniać stosowane przyrządy, kolejność wykonywania pomiarów, osobę wykonującą pomiar.

Należy bardzo krytycznie sprawdzać prawidłowość zastosowanej metody pomiarów. Jeśli nie mamy wpływu na wybór metody należy starać się oszacować błąd wnoszony przez wadliwą metodę i wprowadzić odpowiednie poprawki do wyników.

---