16-03-99	Konrad Witecki	Wydział Mechaniczny
O8	Wyznaczanie stałej Stefana - Boltzmana.
Kolokwium:	Ocena:		Data:	Podpis:
Wykonanie:

1. Teoria.

Każde ciało o temperaturze wyższej od zera absolutnego, emituje falę elektromagnetyczną. Jeżeli ciało to znajduje się w równowadze termodynamicznej, to takie promieniowanie nazywamy promieniowaniem cieplnym lub temperaturowym, gdyż odbywa się ono kosztem chaotycznego cieplnego ruchu cząsteczek. Promieniowanie cieplne padające na dowolnego ciało, może być przez nie odbite, pochłonięte lub przepuszczone. To samo ciało może być jednocześnie źródłem promieniowania cieplnego. Zdolność emisyjną ciała, znajdującego się w równowadze dynamicznej, definiujemy jako wielkość:

gdzie:

dW_wypr - energia wypromieniowana w jednostce czasu z jednostkowej powierzchni ciała w przedziale długości

Natomiast zdolność absorpcyjna ciała jest zdefiniowana w następujący sposób:

tzn. a_T(λ) określa, jaka część energii fali elektromagnetycznej o długościach zawartych w przedziale (λ;λ+Δλ) padającej w jednostce czasu na jednostkową powierzchnię, zostaje pochłonięta. Z doświadczenia wynika, że zdolność emisyjna i zdolność absorpcyjna ciała stałego, zależą od długości emitowanych i pochłanianych fal, temperatury ciała i rodzaju jego powierzchni. Ciało, które absorbuje całe padające na nie promieniowanie (a_T(λ)) nazywamy ciałem czarnym.

Zdolność emisyjna ciała czarnego (ε_T(λ)) zależy od λ i temperatury bezwzględnej ciała T. Wielkość ε_T(λ) oznacza energię, zawartą w promieniowaniu o długościach fal w przedziale (λ;λ+Δλ) emitowaną przez jednostkową powierzchnię w jednostce czasu, a więc funkcja ε_T(λ) określa rozkład widmowy promieniowania ciała czarnego.

Energia promieniowania o danej długości fali wzrasta ze wzrostem temperatury a długość fali odpowiadającej maksymalnej energii promieniowania dąży do mniejszych wartości. Iloczyn λ_max*T ma stałą wartość:

Powyższy związek znany jest jako prawo przesunięć Wiena. Jakościowym potwierdzeniem tego prawa mogą być obserwacje zmian barwy świecenia ciał rozżarzanych do coraz wyższej temperatury. Barwa świecenia przesuwa się od czerwieni poprzez żółtą do niebieskawej, co jest związane z tym, że w miarę wzrostu temperatury, maksimum natężenia świecenia przesuwa się coraz bardziej w stronę fal krótkich.

Podobnie jak prawo Wiena, na podstawie danych doświadczalnych, znaleziono zależność całkowitej zdolności emisyjnej ciała czarnego od temperatury (prawo Stefana - Blotzmana):

gdzie:

I_T - całkowita energia emitowana z wszystkimi długościami w jednostce czasu z jednostkowej powierzchni ciała (całkowita zdolność emisyjna ciała),

T - temperatura [K]

- stała Stefana - Blotzmana.

Boltzman stosując metody termodynamiki do badania promieniowania cieplnego, wykazał słuszność empirycznego wzoru Stefana. Zawiodły wszystkie próby wyprowadzenia w oparciu o prawa klasyczne równania, opisującego rzeczywisty przebieg krzywej rozkładu energii.

Jedną z bardziej znanych prób powiązania teorii z doświadczeniem, była tzw. teoria Rayleigha - Jeansa. Rozpatrywali oni wnękę ze ściankami metalicznymi, wypełnioną promieniowaniem cieplnym. W równowadze promieniowania to ma rozkład widmowy ciała czarnego, charakterystyczny dla temperatury T. W stanie stacjonarnym promieniowanie elektromagnetyczne wewnątrz wnęki musi istnieć w postaci fal stojących z punktami węzłowymi na metalicznych ściankach. Z energetycznego punktu widzenia promieniowanie to jest równoważne nieskończonej liczbie nie oddziałujących ze sobą, promieniujących oscylatorów harmonicznych, których energia średnia wynosi kT. Badając stany równowagi układu oscylatorów metodami fizyki statystycznej, otrzymali następujące wyrażenia na rozkład widmowy:

Równanie to opisuje rozkład widmowy dla długich fal, lecz dla fal w przybliżeniu λ_max i mniejszych daje wartości znacznie przekraczające wyniki eksperymentalne. Najpoważniejszy zarzut z jakim spotyka się teoria, dotyczył wniosku, że dla bardzo małych długości fal całkowita energia dąży do nieskończoności. Wniosek ten jest znany jako „katastrofa ultrafioletowa”.

Problemem bardzo istotnym jest sam pomiar temperatury. Najczęściej ze względu na zbyt wysokie temperatury musimy stosować metody optyczne pomiaru T oparte na obserwowaniu zdolności emisyjnej ciała. Przyrządy służące do tego rodzajów pomiarów nazywamy pirometrami.

Zasada działania pirometru polega na porównaniu natężenia promieniowania w jakiejś wydzielonej części widma z natężeniem w tym samym przedziale długości fal ciała czarnego zmieniamy do chwili, kiedy oba natężenia się zrównają. Zasadniczą częścią pirometru jest żarówka P, natężenie wysyłanego przez nią światła możemy zmienić za pomocą oporu regulacyjnego. Soczewki S₁ i S₂ odgrywają rolę obiektywu i okularu, filtr czerwony (f_cz) służy do monochromatyzacji a przy pomocy filtru szarego (f_sz) zmieniamy zakres przyrządu. Przez pirometr spoglądamy na ciało, którego temperaturę chcemy zmierzyć i zmieniamy natężenie światła żarówki P dotąd, dopóki obraz jej nitki nie zniknie na tle świecącego ciała. Przyrząd wzorcujemy uprzednio za pomocą ciała czarnego o znanych temperaturach, otrzymując krzywą dającą zależność między natężeniem prądu w żarówce P a temperaturą ciała czarnego.

2. Przyrządy.

• ława optyczna

• 4 koniki

• obiektyw MIKAR-S w uchwycie

• układ: zwierciadło płaskie + matówka

• pirometr optyczny

• woltomierz elektromagnetyczny 0-60V

• amperomierz elektromagnetyczny 0-5A

• panel „zasilanie sieciowe”

• panel „autotransformator regulowany”

• panel „stabilizator napięcia”

• lupa

3. Sposób wykonania ćwiczenia.

Wykonanie ćwiczenia składa się z dwóch punktów. Pierwszym z nich jest pomiar wielkości fizycznych żarnika żarówki. W tym celu na ławie optycznej budujemy układ umożliwiający projekcję powiększonego obrazu żarnika. Obraz ten oglądamy na matówce. Następnie przy użyciu lupy z podziałką mierzymy: d, d', h, oraz x+y. Na podstawie tych
pomiarów obliczamy powierzchnię żarnika , korzystając ze wzoru:

Drugi punkt pomiarowy to wyznaczanie stałej Stefana-Blotzmmana, którą to obliczamy w oparciu o wzór:

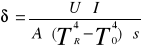
Gdzie:

s - powierzchnia włókna żarnika

To - temperatura pokojowa

Wartości potrzebnych nam wielkości otrzymujemy poprzez następujące czynności:

• Zamocować na ławie żarówkę w obudowie, obiektyw MIKAR-S w obudowie i pirometr optyczny tak aby włókno żarnika znajdowało się na osi optycznej obiektywu i pirometru.

• Łączymy układ zasilający żarówkę.

• Pokrętłem autotransformatora ustawiamy napięcie U=1V.

• Regulując położenie obiektywu ustawimy ostry obraz włókna żarówki.

• Obracając pokrętło pirometru uzyskujemy zrównanie luminacji włókna żarówki pirometrycznej i żarówki badanej (obraz żarówki pirometrycznej przestaje być widoczny na tle włókna badanej żarówki).

• Odczytujemy wartość napięcia, natężenia oraz wartość temperatury czarnej. Pomiary te wykonujemy osiem razy.

• Zwiększając napięcie zasilające żarówkę co 0,2V przeprowadzamy powyższe pomiary.

4. Pomiary i obliczenia.

Lp.	U	I	Tcz	Tczśr	ΔTcz	A	TR	δ	Δδ
	V	A	C	K			K
1	2	5,71	1860	2821,25		0,438	1860,069	2,12E-14
2	2,2	6,56	2020	2821,25		0,435	2020,076	1,93E-14
3	2,4	6,82	2400	2821,25		0,4275	2400,092	1,12E-14
4	2,6	7,15	2650	2821,25		0,4235	2650,103	8,64E-15
5	2,8	7,42	2900	2821,25		0,4175	2900,114	6,83E-15
6	3	7,6	3240	2821,25		0,411	3240,13	4,89E-15
7	3,2	7,91	3510	2821,25		0,404	3510,144	4,01E-15
8	3,4	8,18	3990	2821,25		0,3965	3990,167	2,69E-15

Pomiary parametrów żarnika:

h	d	d'	n	S
0,5	2	0,2	26	102,9684

1

4

---