Zadanie 1

Mamy 5 kul białych i 3 kule czarne. Losujemy dwie kule. Mamy obliczyc prawdopodobieństwa:

1. Wylosowania kul białych

2. Wylosowania kul jednakowego koloru

3. Wylosowania kul różnokolorowych

Istnieja dwa sposoby rozwiązania. Oto pierwszy z nich:

a)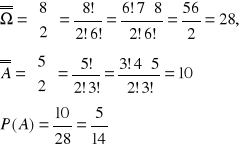

b)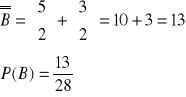

c)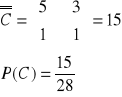

Ale można także drugim sposobem a mianowicie:

Zadanie 2

Sześciu mężczyzn i dwie kobiety losowo ustawiło się w kolejce. Jakie jest prawdopodobieństwo, że panie będą stały obok siebie?

Zadanie domowe 1 (nieobowiązkowe):

Ośmiu mężczyzn i dwie kobiety losowo ustawiło się w kolejce. Jakie jest prawdopodobieństwo, że pomiędzy nimi będzie dokładnie pięciu mężczyzn?

Zadanie 3

W pewnym mieście 80% rodzin ma pralke automatyczną P. 50% ma zmywarkę Z, a 40% ma i pralkę i zmywarkę
. Jakie jest prawdopodobieństwo, że losowo wybrana rodzina w tym mieście będize miała przynajmniej jedno z tych urządzeń?

Obliczamy:

Zadanie 4

Z przedziału Z od [-300, 300] losowo wybieramy dwie liczby b i c. Należy obliczyć prawdopodobieństwo, że równanie
ma pierwiastki rzeczywiste.

Rozważmy zadanie graficznie:

, czyli pole całego kwadratu. Liczymy dalej:

. Miara A =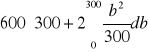

po odpowienim podzieleniu.

Zadanie domowe 2:

Dwie osoby losowo przychodzą na umówione miejsce spotkania w ciągu godziny. Obliczyć należy prawdopodobieństwo spotkania się tych osób, jeśli osoba, która przybędzie pierwsza czeka kwadrans i odchodzi.

Zadanie 5

Wiemy, że
. Należy obliczyć
, a dodatkowo w domu nastepujące przykłady:

a)

b)

Zadanie 6

W skrzyni jest 12 detali wyprodukowanych w zakładzie A, 20 w zakładzie B i 18 w zakładzie C. Wadliwość produkcji poszczególnych zakładów wynosi dla A - 10%, dla B - 40% i dla C - 10 %.

1. Obliczyć prawdopodobieństwo, że losowo wybrany detal będzie dobry

2. Wylosowany detal okazał się wadliwy. Jakie jest prawdopodobieństwo, że wyprodukował go zakład B?

a) Załóżmy, że D to dobry detal, a W - detal wadliwy.

b)

Zadanie domowe 3:

53% studiujących w pewnej uczelni to panie. Wiadomo, że 9% pań i 12% panów niezaliczyło sesji. Obliczyć prawdopodobieństwo, że losowo wybrany student z tej uczelni nie zaliczył sesji.

c

b

300

-300

300

-300

Zbiór zdarzeń sprzyjających. Granicę górną wyznacza parabola.

bez części wspólnej

---