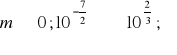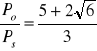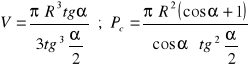ROZWIĄZANIA ZADAŃ
Funkcja liniowa
a)
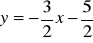
, b)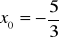
, c)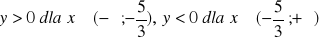
d) prosta równoległa:![]()
prosta prostopadła: ![]()
równoległa dla a=2,25; prostopadła dla a=
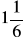
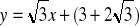
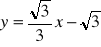
a) z osią OX: (6;0), z osią OY: (0;3)
b) prosta równoległa: ![]()
prosta prostopadła: ![]()
6. a) m<2, b) m>2, c) m=2, d) nie istnieje takie m, e) m=2
a)
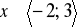
, b)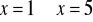
8. a) ![]()
, b) ![]()
9. a) ![]()
, b) ![]()
, c) ![]()
, d) ![]()
e) ![]()
10. ![]()
b) P = 22,5
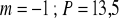
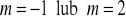
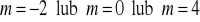
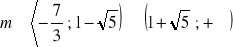
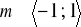
17.a) ![]()
, b) 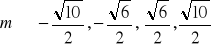
18. ![]()
19. a) ![]()
, b) ![]()
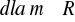
układ ma jedno rozwiązanie: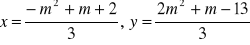
a) ![]()
, b) m = 3 lub m = -3
21. a) ![]()
, b) ![]()
a)
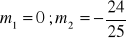
, b)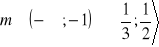
23. dla ![]()
układ równań ma jedno rozwiązanie: ![]()
a) ![]()
, b) ![]()
układ
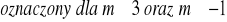
, układ nieoznaczony dla m = 3,
układ sprzeczny dla m = -1
dla
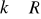
układ ma jedno rozwiązanie: x = 1; y = -k + 3
a) ![]()
, b) ![]()
26. ![]()
27. ![]()
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
33. ![]()
Funkcja kwadratowa
1. ![]()
2. ![]()
3. ![]()
4. ![]()
a)
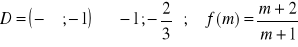
b) ![]()
c) 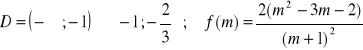
d) 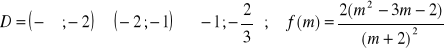
e) 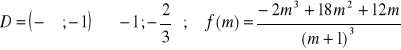
f) 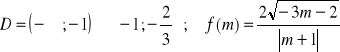
6. a) ![]()
, b) ![]()
7. 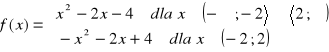
![]()
brak rozwiązania
![]()
jedno rozwiązanie
![]()
dwa rozwiązania
![]()
lub ![]()
trzy rozwiązania
![]()
cztery rozwiązania
8. 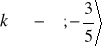
9. wsk. : f (m) = m2 - 6m + 5 dla m![]()
a)
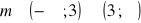
, b)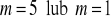
11. 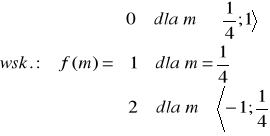
12. 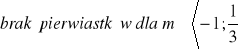
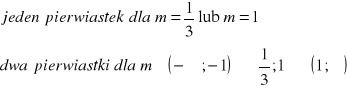
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. b = -5
a) 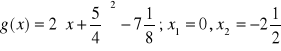
, b) ![]()
24. a) dwa rozwiązania dla ![]()
, jedno rozwiązanie dla m = -4 lub m = 4,
brak rozwiązania dla ![]()
; dwa pierwiastki ujemne dla ![]()
b) ![]()
a) ![]()
, b) g (x) = ![]()
; ![]()
b = 10,
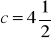
a) 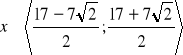
, b) ![]()
b = 4
a) wartość największa równa 3 dla x = 1; wartość najmniejsza równa 1 dla x = 0
b) wartość wyrażenia wynosi -5
c) równanie osi symetrii: ![]()
; zbiór wartości Y = ![]()
a)
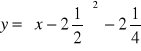
, b) wartość najmniejsza równa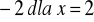
29. b = 2, c = 1
wartość wyrażenia wynosi
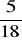
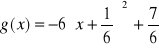
; funkcja g (x) osiąga wartość najmniejszą równą -3 dla x = -1
30. b = -2,c = -12
a) 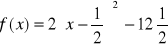
; wartość wyrażenia wynosi ![]()
, b) ![]()
31. c = 4
a) ![]()
, b) ![]()
b = -4, c = 1
a) wartość wyrażenia wynosi 27, b) ![]()
a)
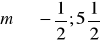
, b)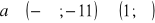
34. ![]()
35. ![]()
36. ![]()
37. ![]()
a)
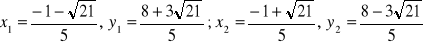
b) ![]()
, c) ![]()
d) ![]()
39. ![]()
40. ![]()
41. ![]()
drugi bok musi być dłuższy o
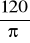
cm12 zawodników
P = 8
punkty styczności: A = (-1, 4) , B = (3, 2);
równania stycznych: y = 2x + 6, y = 2x - 4
w 13-kącie.
Wielomiany
a)
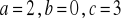
, b)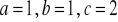
2. a) ![]()
, b) ![]()
3. a) ![]()
b) ![]()
a)
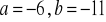
, b)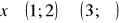
a)
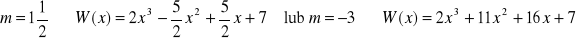
b) 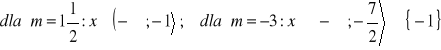
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
pierwiastek, ![]()
dwa pierwiastki,
dla p![]()
trzy pierwiastki
22. ![]()
23. ![]()
24. ![]()
25. ![]()
![]()
![]()
Funkcja wymierna
a)
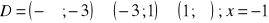
, b)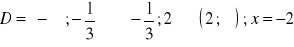
a)
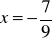
, b)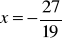
a)
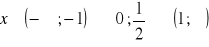
, b)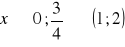
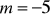
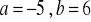
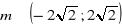
a)
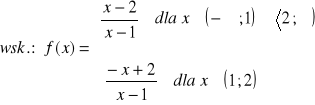
b) 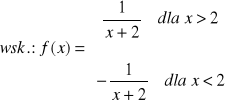
a)
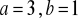
, b)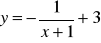
dwa różne rozwiązania dla
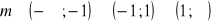
; jedno rozwiązanie dla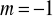
lub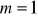
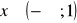
Ciągi
a)
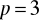
, b)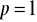
ciąg malejący ;
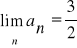
a)
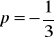
, b) wsk. : wykres ciągu jest punktowy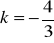
a) nie, b) tak
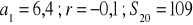
a)
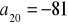
, b)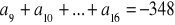
, c)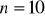
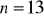
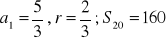
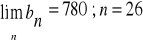
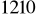
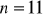
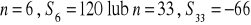
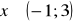
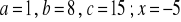
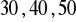
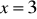
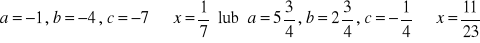
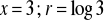
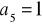
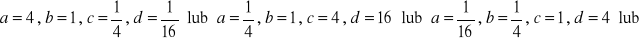
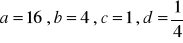
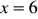
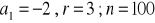
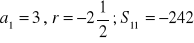
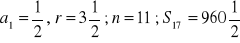
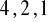
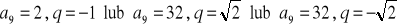
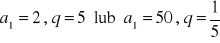
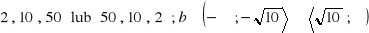
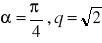
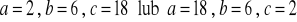
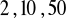
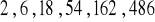
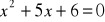
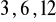
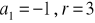
a) ![]()
, b) ![]()
a)
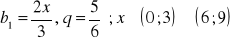
b) ciąg malejący ![]()
jest ciągiem arytmetycznym
a) ![]()
, b) ![]()
ciąg geometryczny o ilorazie
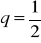
a) ![]()
, b) ![]()
a) ![]()
, b) ![]()
a)
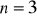
, b)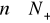
, c)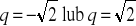
a)
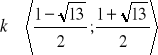
, b)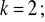
ciąg rosnący, c)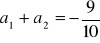
, d) żaden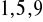
lub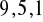
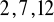
lub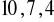
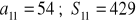
ciąg geometryczny
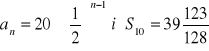
;
ciąg arytmetyczny ![]()
ciąg geometryczny:
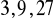
; ciąg arytmetyczny: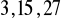
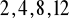
lub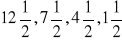
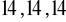
lub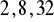
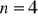
lub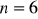
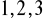
lub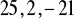
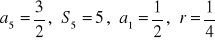
a)
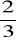
, b)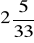
, c)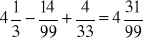
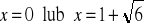
a)
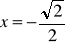
, b)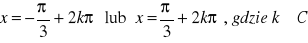
, c) równanie nie ma rozwiązania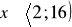
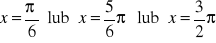
Funkcje trygonometryczne
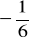
a)
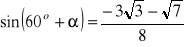
, b)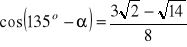
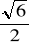
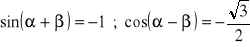
a)
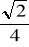
, b)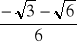
, c)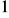
a)
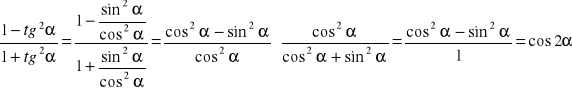
b) ![]()
c) ![]()
a)
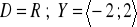
, b)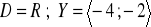
, c)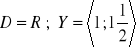
a)
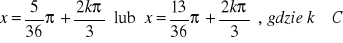
, b)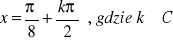
c) ![]()
d) ![]()
e) ![]()
, f) ![]()
a)
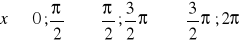
, b)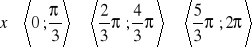
c) ![]()
, d) ![]()
Funkcja wykładnicza i logarytmiczna
a)
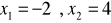
, b)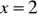
, c)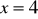
, d)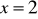
a)
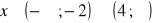
, b)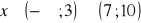
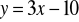
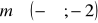
wsk.:
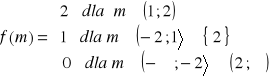
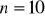
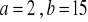
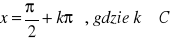
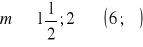
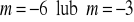
a)
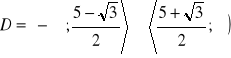
, b)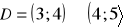
, c)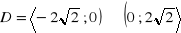
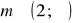
a)
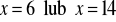
, b)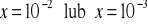
, c)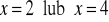
a)
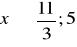
, b)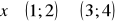
a)
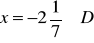
- równanie nie ma rozwiązania, b)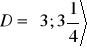
c) przesunięcie o wektor ![]()
, symetria wzgl. osi OX , przesunięcie o wektor ![]()
Geometria analityczna
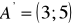
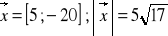
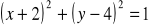
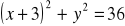
a)
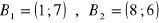
, b)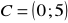
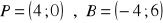
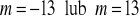
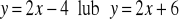
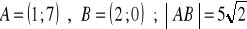
a)
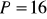
, b)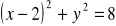
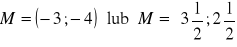
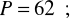
równanie wysokości: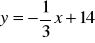
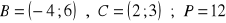
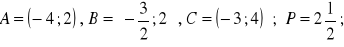
równanie okręgu: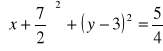
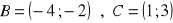
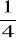
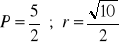
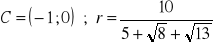
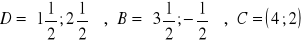
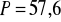
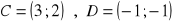
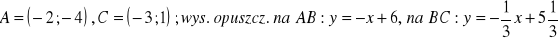
a)
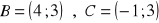
, b)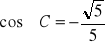
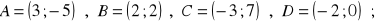
długość boku: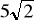
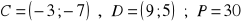
Planimetria
a)
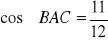
, b)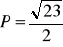
, c)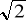
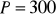
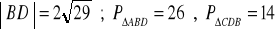
obwód trapezu:
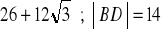
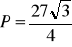
krótsza podstawa 14 i ramię 30 lub krótsza podstawa 34 i ramię 20
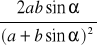
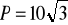
obwód trójkąta:
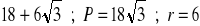
a) obwód:
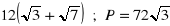
b) kąt przekątnej z dłuższym bokiem: ![]()
z krótszym bokiem: ![]()
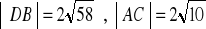
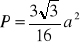
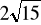
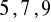
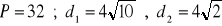
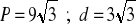
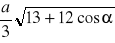
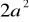
a)
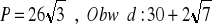
, b)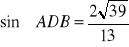
, c)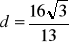
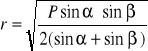
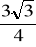
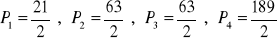
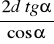
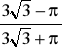
a)
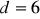
, b)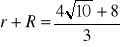
a)
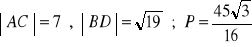
, b)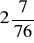
a)
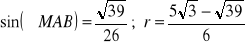
, b)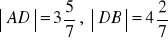
a)
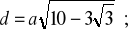
stosunek pól: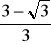
, b)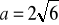
a)
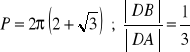
, b)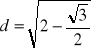
środkowa
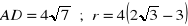
a)
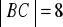
, b)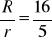
Stereometria
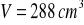
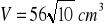
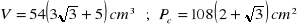
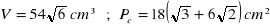
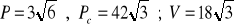
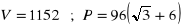
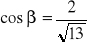
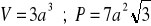
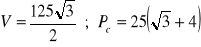
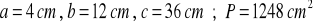
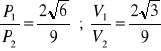

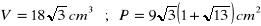
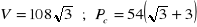
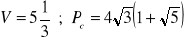
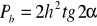
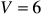
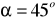
a)
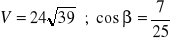
, b)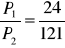
a)
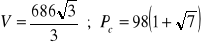
, b)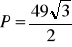
a)
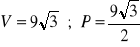
, b)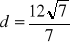
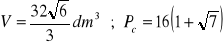
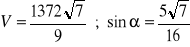
a)
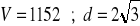
, b)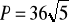
a)
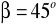
, b)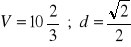
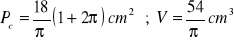
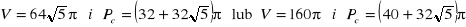
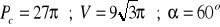
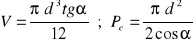
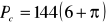
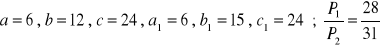
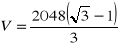
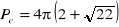
z 14 pomarańczy
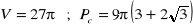
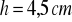
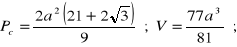
długość krawędzi: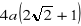
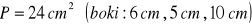
a)
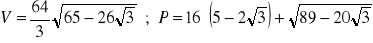
b) ![]()
![]()
- kąt nachylenia ściany bocznej do podstawy)
![]()
-kąt nachylenia krawędzi bocznej do podstawy)
Rachunek prawdopodobieństwa
a)
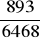
, b)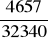
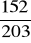
a)
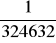
, b)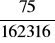
, c)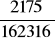
a)
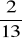
, b)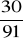
, c)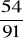
, d)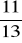
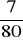
a)
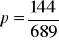
, b)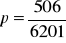
, c)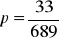
a)
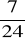
, b)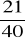
, c)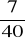
a)
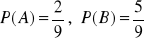
, b) Trzeba dodać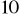
czarnych kul
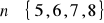
pierwszy sposób
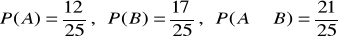
a)
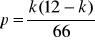
, b)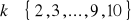
a)
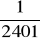
, b)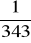
, c)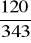
zdarzenia
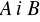
są niezależnea) zdarzenia są zależne , b)
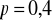
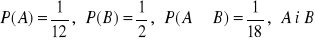
są zależnea)
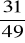
, b)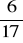
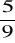
, 19.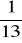
, 20.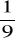
, 21.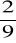
, 22.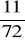
, 23.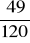
, 24.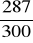
, 25.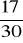
a)
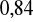
, b)
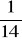
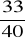
Bliższe spełnienia jest marzenie Wojtka
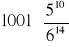
a)
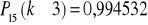
b) ![]()
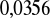
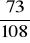
Są dwie kule białe
a)
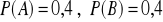
b) Zdarzenia![]()
są zależne
Granica, ciągłość i pochodna funkcji
a)
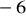
, b)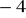
a)

, b)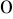
, c)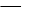
, d)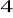
, e)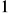
, f)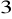
, g)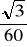
funkcja nie jest ciągła
a)
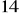
, b)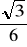
a)
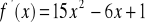
, b)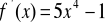
, c)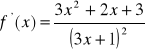
d) ![]()
, e) ![]()
, f) ![]()
g) ![]()
, h) ![]()
i) 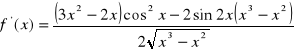
, j) ![]()
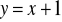
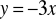
a)
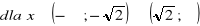
funkcja jest rosnąca
![]()
funkcja jest malejąca
b) ![]()
funkcja jest rosnąca
![]()
funkcja jest malejąca
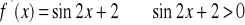
dla każdego x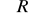
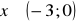

a)
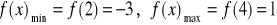
b) ![]()
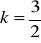
a) wartość największa wynosi
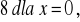
wartość najmniejsza wynosi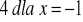
lub x=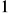
b) wartość największa wynosi ![]()
wartość najmniejsza wynosi ![]()
wartość największa wynosi
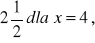
wartość najmniejsza wynosi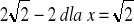
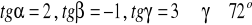
odcinek należy podzielić na dwie równe części po 9 każda
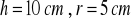
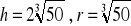
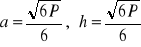
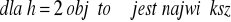

91
Wyszukiwarka
Podobne podstrony:
rozwiazywanie zadan tekstowych wb
efekt plejotropowy rozwiazanie zadań 1
cw8s rozwiazania zadan new id 123854
Metodyka rozwiązywania zadań, Transport Politechnika, Semestr 1, Fizyka
Rozwiązania zadań sprawdzających EKONOMIA działy 1-4, UP, ekonomia
Octan izoamylu rozwiązanie zadań
dodawanie rozwiazywanie zadań
38 Olimpiada Wiedzy Technicznej I Stopień Rozwiązania Zadań
dynamika 10 zadań z rozwiązaniami
Logika rozwiazania zadan id 272023
GM P1 142 Rozwiazania zadan i s Nieznany
CIĄGI – rozwiązanie zadań
Chromatografia rozwiązania zadań
27 Wyjaśnić znaczenie odchylenia linii pionu w rozwiązywaniu podstawowych zadań geodezyjnych
GM M1 142 Rozwiazania zadan i s Nieznany
Rozwiązanie zadań na energię elektronów w przeskokach
więcej podobnych podstron