Ćwiczenie 21
Pomiar ogniskowej cienkich soczewek metodą Bessela.
Podstawa teoretyczna
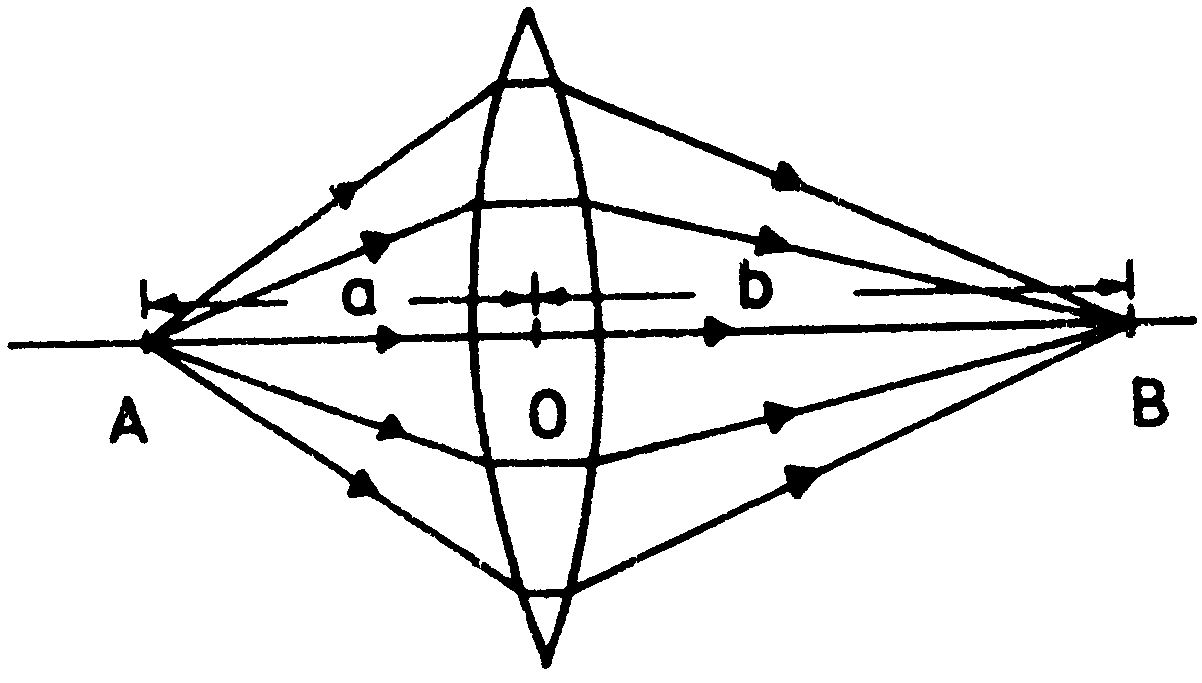
Soczewką nazywamy bryłę z przezroczystego materiału, ograniczoną powierzchniami kulistymi, parabolicznymi lub walcowymi. Rozróżniamy dwa zasadnicze typy soczewek: zbierające i rozpraszające. Soczewki zbierające są w środku grubsze niż na brzegach, rozpraszające - przeciwnie - grubsze na brzegach niż na środku.
Wiązka promieni wychodzących ze świecącego punktu A na osi optycznej soczewki skupiającej po przejściu przez soczewkę zostaje zebrana w punkcie B zwanym obrazem rzeczywistym punktu A (rysunek 1). Odległości punktu A i jego obrazu B od środka soczewki spełniają zależność zwaną wzorem soczewkowym:
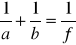
,
gdzie: f - ogniskowa soczewki.
Ogniskowa soczewki wyraża się wzorem:
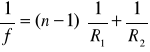
,
gdzie: n - jest współczynnikiem załamania materiału soczewki względem otaczającego ośrodka, R1 i R2 - są promieniami krzywizny powierzchni soczewki.
Ogniskową układu fu dwóch cienkich soczewek o ogniskowych f i f', umieszczonych blisko siebie, można obliczyć ze wzoru:
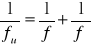
.
Ogniskową soczewki skupiającej można wyznaczyć bezpośrednio ze wzoru (1), mierząc odległość przedmiotu od soczewki a oraz odległość soczewki b (metoda bezpośrednia). Dla soczewek grubych oraz układów soczewek wyznaczanie ogniskowej metodą bezpośrednią jest utrudnione i mało precyzyjne. Trudności te można ominąć wyznaczając ogniskową soczewki metodą Bessela.
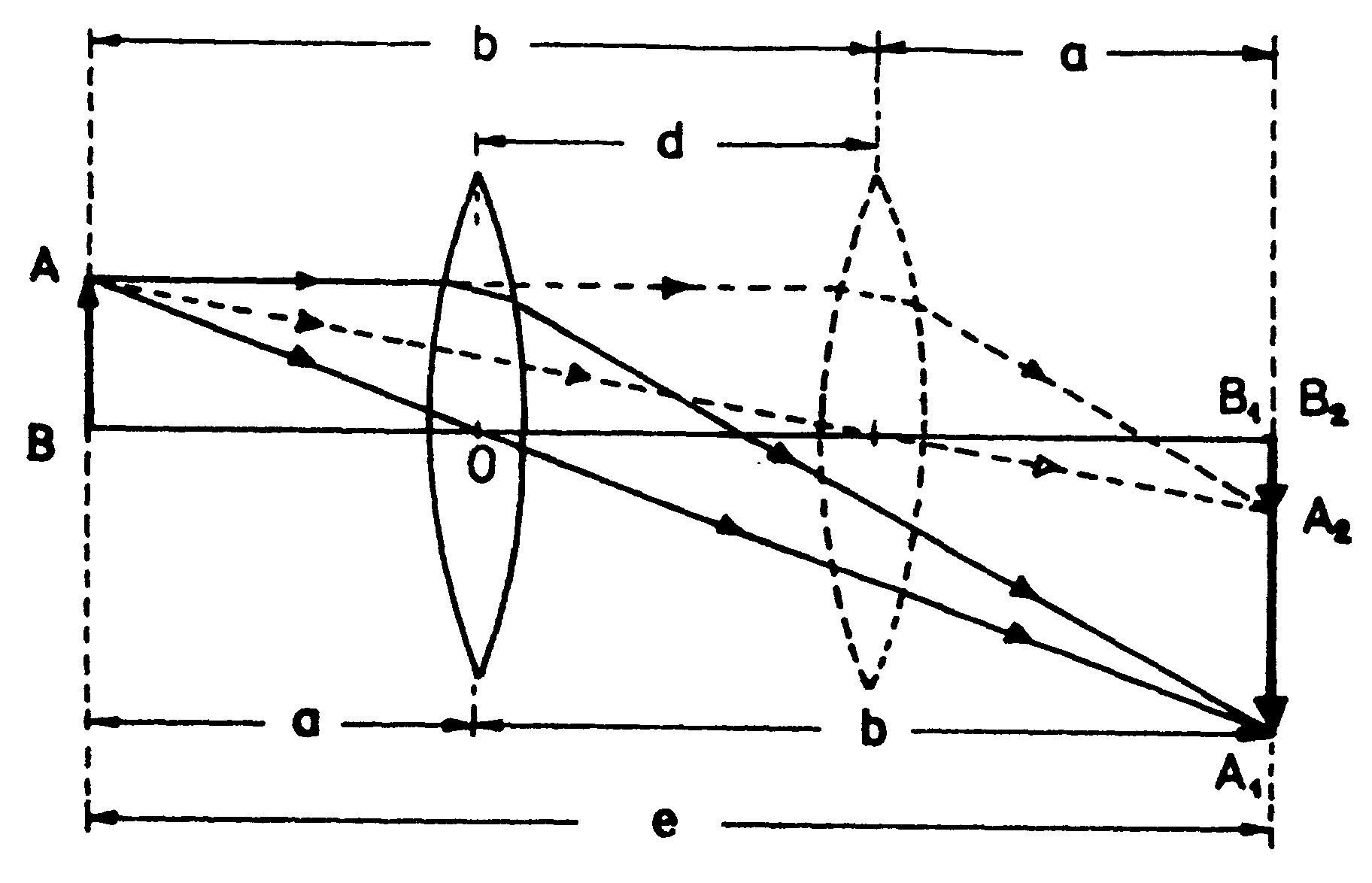
Z rysunku 2 i wzoru (1) możemy wyprowadzić wzór na ogniskową soczewki:
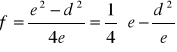
.
Dla otrzymania dwóch obrazów rzeczywistych odległość przedmiotu od ekranu musi spełniać warunek e>4f, jak wynika z ostatniego wzoru.
Określając metodą Bessela ogniskową fu układu soczewek możemy obliczyć ogniskową soczewki rozpraszającej ze wzoru (3), przyjmując f'=fr:
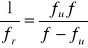
.
Ze wzoru (3) wynika, że układ soczewek będzie miał własności skupiające (fu>0), jeżeli ogniskowe poszczególnych soczewek spełniają nierówność ![]()
.
Cel i przebieg doświadczenia
Zadaniem doświadczenia jest obliczenie ogniskowych kolejno: dwóch soczewek zbierających, układu soczewki zbierającej z rozpraszającą i wreszcie samej soczewki rozpraszającej.
Na ławie optycznej pomiędzy wąską oświetloną szczeliną w kształcie strzałki (przedmiotem) a ekranem umieszczamy soczewkę skupiającą . Przedmiot i ekran oddalone są od siebie o e (istotne dla metody Bessela). Przesuwamy soczewkę do momentu, aż uzyskamy na ekranie ostry, powiększony i odwrócony obraz. Notujemy uzyskaną na podziałce ławy odległość przedmiotu od soczewki a oraz ekranu od soczewki b (do metody bezpośredniej). Następnie przesuwamy soczewkę ku ekranowi, by otrzymać ostry, odwrócony, lecz tym razem pomniejszony obraz przedmiotu. Mierzymy odległość soczewki od przedmiotu b i od ekranu a, a także przesunięcie soczewki względem poprzedniego położenia. Dla większej precyzji doświadczenie przeprowadzamy trzykrotnie.
Kolejno bierzemy drugą z soczewek skupiających () i dokonujemy identycznych pomiarów. Aby uzyskać ostry obraz należało zmienić odległość e.
Następnie na ławie umieszczamy układ soczewek δ (tę z dwóch soczewek skupiających, która ma mniejszą ogniskową () oraz soczewkę rozpraszającą γ) i, po dostosowaniu odległości e, dokonujemy pomiarów analogicznych jak w przypadku soczewek skupiających.
Wyniki doświadczenia
Soczewka skupiająca
Soczewka skupiająca
Układ δ: soczewka skupiająca + soczewka rozpraszająca γ
Metody obliczania błędów pomiaru
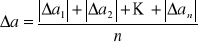
,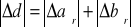
.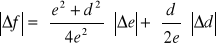
.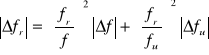
.Obliczenia
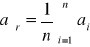
, analogicznie bśr i dśr,Soczewka skupiająca
e = 560
aśr = 224,7
bśr = 335,3
dśr = 110,7
błąd odległości
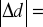
4,2, czyli błąd względny wyniósł 3,82%fbezpośrednie = 134,5
fBessel = 134,5
błąd ogniskowej
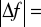
0,68, czyli błąd względny wyniósł 0,5%Soczewka skupiająca
e = 225
aśr = 77,8
bśr = 147,2
dśr = 69,3
błąd odległości
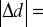
3,7, czyli błąd względny wyniósł 5,29%fbezpośrednie = 50,9
fBessel = 50,9
błąd ogniskowej
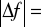
0,84, czyli błąd względny wyniósł 1,65%Układ δ: soczewka skupiająca + soczewka rozpraszająca γ
e = 450
aśr = 128,5
bśr = 321,5
dśr = 193
błąd odległości
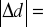
11,7, czyli błąd względny wyniósł 6,04%fbezpośrednie = 91,8
fBessel = 91,8
błąd ogniskowej
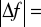
2,8, czyli błąd względny wyniósł 3,05%Soczewka rozpraszająca γ
fr = -114,3
błąd ogniskowej
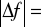
8,56, czyli błąd względny wyniósł 7,49%Analiza błędów
Wnioski
L.p. |
Odległość |
a |
b |
d |
1. |
560 |
225 |
335 |
108 |
|
560 |
227 |
333 |
|
2. |
560 |
221 |
339 |
112 |
|
560 |
227 |
333 |
|
3. |
560 |
222 |
338 |
112 |
|
560 |
226 |
334 |
|
L.p. |
Odległość |
a |
b |
d |
1. |
225 |
76 |
149 |
70 |
|
225 |
79 |
146 |
|
2. |
225 |
76 |
149 |
68 |
|
225 |
81 |
144 |
|
3. |
225 |
76 |
149 |
70 |
|
225 |
79 |
146 |
|
L.p. |
Odległość |
a |
b |
d |
1. |
450 |
135 |
315 |
193 |
|
450 |
122 |
328 |
|
2. |
450 |
132 |
318 |
194 |
|
450 |
124 |
326 |
|
3. |
450 |
136 |
314 |
192 |
|
450 |
122 |
328 |
|
Błędy pomiaru odległości aśr oblicza się jako błąd przeciętny ze wzoru:
gdzie: a = A - an i A jest wartością rzeczywistą mierzonej wielkości (za A można uznać wartość średnią odległości a). Identycznie wyznacza się błąd pomiaru bśr.
Błąd odległości e od przedmiotu od ekranu oceniamy na podstawie dokładności skali ławy optycznej. W opisywanym doświadczeniu wynosił on 1mm.
Błąd odległości d obliczamy ze wzoru:
Błąd ogniskowej f soczewki skupiającej znajdujemy posługując się wzorem:
Błąd ogniskowej układu soczewek fu obliczamy jak błąd ogniskowej pojedynczej soczewki. Błąd ogniskowej soczewki rozpraszającej fr znajdujemy ze wzoru:
Ogniskową bezpośrednio obliczamy ze wzoru (1), metoda Bessela - korzystamy ze wzoru (4).
Jak zaznaczono w punkcie IV błąd związany ze skalą ławy optycznej wyniósł 1 mm.
Zwraca uwagę duża, w porównaniu z soczewkami i , wartość błędu względnego ogniskowej układu soczewek i soczewki γ. Jest to błąd systematyczny mający swoje źródło w mało stabilnym uchwycie soczewek, na który przeprowadzający pomiary mieli niewielki wpływ.
Powodem dodatkowo wpływającym na spore (choć przecież nie aż tak znaczne) rozbieżności w wynikach miała niedoskonałość przyrządu optycznego, jakim jest ludzkie oko. W związku z tym każdy z obserwujących obraz mógł przy innym ustawieniu soczewki odbierać go jako ostry.
Metoda pomiaru ogniskowej soczewek zaproponowana przez Friedricha Wilhelma Bessela daje rezultaty zgodne ze wzorem soczewkowym Newtona. Jednocześnie pozwala w stosunkowo łatwy sposób obliczać ogniskowe układu soczewek. Występujące przy tym odchylenia oscylują dość blisko wartości średniej, zwłaszcza istotna jest „odporność” na błędy przypadkowe. Dzięki tej metodzie również jesteśmy w stanie wyznaczyć pośrednio ogniskową soczewki rozpraszającej poprzez zestawienie jej w układ z soczewką skupiającą. Wszystko to plus zalety dydaktyczne pozwalają określić metodę Bessela jako przydatną.
Wszystkie wyniki w mm.
Ostateczne wyniki w[mm] zostały podane z precyzją jednego miejsca po przecinku, wartości procentowe - dwóch miejsc po przecinku.
2
4
Rysunek 1
Rysunek 2
Wyszukiwarka
Podobne podstrony:
pomiar ogniskowej cienkich soczewek metodą Bessela
Pomiar ogniskowej soczewek metodą Bessela, LAB 21V2, LABORATORIUM FIZYCZNE
Ćw. 6 Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego i metodą Bessela, PWSZ, Fizyka laborki
Fizyka 6 - Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego i metoda Bessela, Studia, Geodezja
WYZNACZANIE ODLEGŁOŚCI OGNISKOWYCH SOCZEWEK METODĄ BESSELA, Sprawozdania - Fizyka
Cw 06 - Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego i metodą Bessela, Sprawozdania fizyka
Wyznaczanie ogniskowej soczewki metodą Bessela, Technologia chemiczna, semestr 2, Fizyka, Laboratori
Wyznaczanie ogniskowej soczewki metodą Bessela, Sprawozdania
badanie ogniskowej soczewki metoda bessela
Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego oraz metodą Bessela, LAB F303, 302
Pomiary ogniskowych soczewek metod Bessela v2, Pracownia Zak˙adu Fizyki Politechniki Lubelskiej
sprawka fizyka, Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego oraz metodą Bessela., nr
Wyznaczanie ogniskowych soczewek ze wzoru soczewkowego oraz metodą Bessela, 303Am, fiza303
więcej podobnych podstron