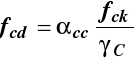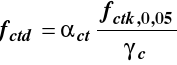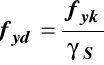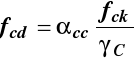WYŻSZA SZKOŁA TECHNICZNO-PRZYRODNICZA

W POZNANIU

DR INŻ. MAŁGORZATA MURKOWSKA

KONSTRUKCJE BETONOWE

ZASADY WYMIAROWANIA

WYKŁADY

Literatura z przedmiotu konstrukcje żelbetowe

1. PN-B-03264:2002 Konstrukcje betonowe, żelbetowe i sprężone

Obliczenia statyczne i projektowanie

2. PN-EN 1992-1-1:2004+AC:2008 Eurokod 2

Projektowanie konstrukcji z betonu

Część 1-1: Reguły ogólne i reguły dla budynków

3. Obliczanie konstrukcji żelbetowych według Eurokodu 2.

M. Knauff, PWN, 2012

4. Przykłady obliczeń elementów zginanych jednokierunkowo

zbrojonych. Zeszyt 1

T. Urban, E. Habiera, Politechnika Łódzka, 2010

5. Konstrukcje żelbetowe wg PN-B-03264:2002 i Eurokodu 2,

tom I, II, III Włodzimierz Starosolski, PWN, 2009

6. Projektowanie elementów żelbetowych

Małgorzata Murkowska,

Wydawnictwo Politechniki Poznańskiej, 2009

7. Podstawy projektowania i algorytmy obliczeń konstrukcji

żelbetowych

A. Łapko, B. Ch. Jensen, Arkady, 2005

8. Projektowanie konstrukcji żelbetowych

M. Kamiński, J. Pędziwiatr, D. Styś,

DWE, Wrocław, 2004

9. Konstrukcje betonowe. Przykłady obliczeń statycznych.

Kalikst Grabiec, PWN, 1996

10. Konstrukcje żelbetowe, tom I-IV

Jerzy Kobiak, Wiesław Stachurski, Arkady, 1984- 1991

WSTĘP

Pierwsze konstrukcje z betonu wzmocnionego wkładkami stalowymi zaczęto wznosić w latach siedemdziesiątych XIX w.

Minęło więc ponad sto lat, kiedy beton zbrojony prętami stalowymi, który można formować w dowolne kształty zrewolucjonizował architekturę.

Dziś konstrukcje żelbetowe stosowane są we wszystkich gałęziach budownictwa.

Podstawowe rodzaje konstrukcji betonowych różniące się mechanizmem pracy oraz zastosowaniem to;

• konstrukcje betonowe

-beton nie zbrojony stalą lub ze zbrojeniem mniejszym od

minimalnego,

zastosowanie: niektóre fundamenty, posadzki, ściany oporowe.

• konstrukcje żelbetowe

-beton wzmocniony celowo rozmieszczonymi prętami ze stali zbrojeniowej,

zastosowanie: we wszystkich dziedzinach budownictwa.

• konstrukcje sprężone

-beton sprężany zazwyczaj cięgnami stalowymi, w

zależności od sposobu przekazania siły sprężającej

rozróżnia się:

-strunobeton,

-kablobeton,

zastosowane: dźwigary i płyty stropowe oraz dachowe o dużych

rozpiętościach, zbiorniki, konstrukcje specjalne.

Z punktu widzenia metod wykonawczych rozróżnia się:

• konstrukcje monolityczne

wykonywane na miejscu wbudowania,

zaletą jest duża sztywność konstrukcji, wadą długi okres realizacji

obiektu,

• konstrukcje prefabrykowane

montowane z fabrycznie wykonanych prefabrykatów,

zaletą jest szybkość realizacji, natomiast wadą mała sztywność konstrukcji,

• konstrukcje monolityczno-prefabrykowane

wykonywane z monolitycznego żelbetu i elementów prefabrykowanych,

które mogą niekiedy spełniać rolę deskowań.

KONCEPCJA ŻELBETU

Polega na stworzeniu takiego połączenia betonu i stali, w którym :

• siły rozciągające przejmuje stal,

• siły ściskające przejmuje beton.

Celowość zespolenia betonu i stali wynika z własności mechanicznych tych materiałów.

WYTRZYMAŁOŚĆ	BETON	STAL
na ściskanie	10-60 MPa	200-600 MPa
na rozciąganie	1-5 MPa

BETON ma wiele cech wspólnych z kamieniem naturalnym.

Podobnie jak kamień zalicza się do materiałów kruchych.

Wytrzymałość betonu na rozciąganie jest niewielka i wynosi około 10% jego wytrzymałości na ściskanie.

Betony o wysokich wytrzymałościach są jeszcze bardziej kruche (patrz tabela).

STAL natomiast posiada wielokrotnie wyższą od betonu wytrzymałość na ściskanie jak i na rozciąganie.

Współpracę obu materiałów zilustrowano na przykładzie belki zginanej swobodnie podpartej.

Rys. Schemat pracy belki swobodnie podpartej

1. betonowej

2. żelbetowej

BELKA BETONOWA ulega zniszczeniu (złamaniu) w sposób nagły, niesygnalizowany pod wpływem niewielkiego obciążenia.

Beton w strefie rozciąganej osiąga bowiem swoją wytrzymałość na rozciąganie, która jest 10 razy mniejsza niż wytrzymałość na ściskanie.

W BELCE ŻELBETOWEJ zarysowanie elementu przebiega stopniowo.

Po pojawieniu się rys w strefie rozciąganej siły rozciągające przejmuje stal. Belka może być nadal obciążana aż do momentu , w którym beton strefy ściskanej osiągnie swoją wytrzymałość na ściskanie.

Odpowiednio dobrane pręty stalowe pozwalają belce przenosić obciążenie, aż do osiągnięcia przez beton wytrzymałości na ściskanie.

W konstrukcjach z betonu zbrojonego ilość stali jest niewielka.

Zbrojenie stanowi zazwyczaj 2-3% całkowitej objętości elementu.

• W konstrukcji żelbetowej 95% objętości stanowi tworzywo betonowe.

• Jakość konstrukcji żelbetowej zależy głównie od jakości betonu.

Z tego względu jakość betonu i jego właściwości są sprawą pierwszej wagi dla projektantów i wykonawców.

WSPÓŁPRACA BETONU I STALI

Cechy mechaniczne obu materiałów są bardzo zróżnicowane ale ich współpraca jest możliwa i celowa.

Istnienie sił przyczepności jest jednym z najważniejszych

warunków poprawnego funkcjonowania żelbetu.

W procesie twardnienia beton silnie przywiera do stali.

Po przyłożeniu obciążenia sąsiednie włókna betonu i stali

mają jednakowe odkształcenia.

Zespolenie obu materiałów pozostaje nienaruszone.

• Współczynniki rozszerzalności liniowej betonu i stali są praktyczne jednakowe.

Naprężenia termiczne, nawet przy dużych różnicach temperatur są małe i nie wywołują szkodliwych odkształceń.

• Beton doskonale chroni stal przed korozją i działaniem ognia

• Stal ogranicza skutki skurczu betonu (zarysowania) oraz pełzania betonu (przyrost odkształceń).

ZALETY I WADY ŻELBETU

ZALETY:

• ŁATWOŚĆ FORMOWANIA w dowolne kształty.

• WYSOKA WYTRZYMAŁOŚĆ I TRWAŁOŚĆ konstrukcji, której czas eksploatacji w zależności od warunków atmosferycznych wynosi 60-150 lat.

• SZTYWNOŚĆ KONSTRUKCJI MONOLITYCZNYCH

ogranicza stosowanie stężeń w płaskich układach prętowych, pozwala konstruować cienkie przekrycia o dużych rozpiętościach oraz układy przestrzenne.

• OGNIOODPORNOŚĆ betonu zwykłego pozwala mu znosić okresowo temp. ok. 500⁰C, przy której odkryta stal traci 50% swojej wytrzymałości.

• ODPORNOŚĆ NA WAHANIA TEMP. I WILGOCI oraz innych wpływów atmosferycznych.

• TANIA KONSERWACJA szczelny beton chroni stal przed korozją i praktycznie nie wymaga konserwacji.

WADY:

• POWSTAWANIE RYS I ODPRYSKÓW W BETONIE.

• PRACOCHŁONNOŚĆ I SEZONOWOŚĆ, długi okres dojrzewania, konieczność starannej pielęgnacji.

• DUŻE ZUŻYCIE DREWNA tylko w konstrukcjach monolitycznych gdy nie stosuje się deskowań do wielokrotnego użytku.

• DUŻA PRZEWODNOŚĆ CIEPLNA I DŹWIĘKOWA

konieczność stosowania specjalnych izolacji termicznych i akustycznych.

• ZNACZNY CIĘŻAR OBJĘTOŚCIOWY BETONU.

• TRUDNOŚCI W PRZEPROWADZANIE ZMIAN I WZMOCNIEŃ.

OGÓŁNE ZASADY PROJEKTOWANIA wg EUROKODÓW

Program Eurokodów konstrukcyjnych obejmuje następujące normy, zwykle składające się z kilku części:

EN 1990 Eurokod 0: Podstawy projektowania konstrukcji

EN 1991 Eurokod 1: Oddziaływania na konstrukcje

EN 1992 Eurokod 2: Projektowanie konstrukcji z betonu

EN 1993 Eurokod 3: Projektowanie konstrukcji stalowych

EN 1994 Eurokod 4: Projektowanie konstrukcji zespolonych

stalowo-betonowych

EN 1995 Eurokod 5: Projektowanie konstrukcji drewnianych

EN 1996 Eurokod 6: Projektowanie konstrukcji murowych

EN 1997 Eurokod 7: Projektowanie geotechniczne

EN 1998 Eurokod 8: Projektowanie konstrukcji poddanych na

oddziaływania sejsmiczne

EN 1999 Eurokod 9: Projektowanie konstrukcji aluminiowych

Eurokod 2 jest sciśle powiązany z innymi Eurokodami, w szczególności z Eurokodem 0 oraz Eurokodem 1.

W EN 1990 podano zasady i wymagania dotyczące bezpieczeństwa, użytkowalności i trwałości.

Określono podstawy ich obliczania i sprawdzania.

Natomiast EN 1991 wraz ze wszystkimi częściami jest przeznaczona do wyznaczania obciążeń na budowle (obciążenia stałe, użytkowe, oddziaływania wiatru i śniegu)

Podstawowe normy do projektowania konstrukcji betonowych

PN-EN 1992-1-1:2004+AC:2008. Eurokod 2: Projektowanie konstrukcji z betonu. Część 1-1: Reguły ogólne i reguły dla budynków

Część 1-2: Reguły ogólne - Projektowanie z uwagi na warunki pożarowe

PN-EN 206-1:2003. Beton. Część 1: Wymagania, właściwości,

produkcja i zgodność

PN-EN 10080:2005. Stal do zbrojenia betonu. Spajalna stal zbrojeniowa. Postanowienia ogólne.

Opracowane w Polsce normy zharmonizowane z Eurokodami mają oznaczenie PN-EN.

W innych krajach np.: DIN-EN Niemcy; BS-EN W. Brytania;

UNI-EN Włochy; DK-EN Dania; CSN-EN Czechy.

BETON

WIADOMOŚCI OGÓLNE

Beton jest materiałem sztucznym powstałym po stwardnieniu mieszaniny, w skład której wchodzą:

• kruszywo - naturalne lub sztuczne,

• cement - najczęściej portlandzki,

• woda - konieczna do wiązania cementu,

• dodatki (do 5% masy cementu) lub domieszki specjalne (do 40% masy cementu),które np. przyspieszają twardnienie, umożliwiają betonowanie w niskich temperaturach

.

Beton należy do materiałów sprężysto-plastycznych o dużej niejednorodności i skomplikowanej strukturze.

Cechy fizyczne i mechaniczne betonu są zmienne w czasie i zależą od:

- wieku betonu,

- warunków cieplno-wilgotnościowych,

- czasu działania i wielkości obciążenia.

Najistotniejsze cechy mechaniczne jak wytrzymałość i odkształcalność będą szczegółowo omówione.

Podstawowa norma zharmonizowana z Eurokodem 2 to wspomniana

PN-EN 206-1, (zastąpiła ona normę PN-88/B-06250 „Beton zwykły”).

Betony stosowane w żelbecie podzielono w zależności od gęstości objętościowej:

Rodzaj betonu	Symbol	Gęstość objętościowa [kg/m^3]
Lekki	CL	800-2000
Zwykły	C	2000-2600
Ciężki	C	>2600

KLASY I WYTRZYMAŁOŚĆI BETONU

Podstawą określenia klasy betonu jest charakterystyczna wytrzymałość betonu na ściskanie.

Wyznaczona zgodnie z normą PN-EN 206-1 na próbkach walcowych 150/300 mm po 28 dniach od wykonania, oznaczona jest symbolem f_ck,cyl.

Norma PN-EN 206-1 wymienia również wytrzymałość charakterystyczną kostkową f_ck,cube badaną na kostkach o boku 150 mm.

Tablica 7- Klasy wytrzymałości na ściskanie betonu zwykłego i betonu ciężkiego (wg PN-EN 206-1)

Klasa wytrzym. na ściskanie	Minimalna wytrzym. charakterystyczna oznaczna na próbkach walcowych fck,cyl N/mm^2	Minimalna wytrzym. charakterystyczna oznaczna na próbkach sześciennych fck,cube N/mm^2
C8/10 C12/15 C16/20 C20/25 C25/30 C30/37 C35/40 C40/50 C45/55 C50/60	8 12 16 20 25 30 35 40 45 50	10 15 20 25 30 37 40 50 55 60

Klasa betonu = minimalna wytrzymałość charakterystyczna oznaczana na walcach lub kostkach

Norma PN-EN 1992-1-1 stosuje analogiczne

oznaczenie klasy betonu.

C fck/fck,cube np. C 20/25

(Uwaga: w powyższej normie charakterystyczną wytrzymałość walcową oznaczono skrótowo jako f_ck )

Wszystkie informacje o betonie podane są w PN-EN 1992-1-1,

w tablicy 3.1, w której wyszczególnione są następujące wytrzymałości: f_ck, f_ck,cube, f_cm, f_ctm, f_ctk,0,05, f_ctk,0,95 oraz podane odpowiednie wzory przeliczeniowe.

Omówione wytrzymałości charakterystyczne używane są

gdy projektujemy konstrukcję w stanach granicznych użytkowalności SGU.

Wytrzymałość obliczeniowa betonu na ściskanie f_cd

używana w obliczeniach stanów granicznych nośności SGN.

Określana jest ze wzoru

α_cc - współczynnik, którego wartość zalecana w Załączniku

krajowym α_cc = 1,0

(wg EC2 może być przyjmowana w przedziale 0,8 do 1,0)

γ_C - częściowy współczynnik dla betonu, którego wartość w

Załączniku krajowym w tab. NA.2 przyjęto γ_C = 1,4

(wg EC2 tab. 2.1N, przyjęto w sytuacjach trwałych i

przejściowych γ_C = 1,5 )

Tak więc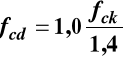

Wytrzymałość betonu na rozciąganie f_ct

Wartość wytrzymałości betonu na rozciąganie zależy od klasy betonu, a więc od wytrzymałości na ściskanie.

Wytrzymałość betonu na rozciąganie wynosi około 10% jego wytrzymałości na ściskanie

Wytrzymałość betonu na rozciąganie f_ct odpowiada maksymalnemu naprężeniu, jakie może przenieść beton pod obciążeniem osiowym.

Tablica 3.1 w PN-EN 1992-1-1 podaje następujące wartości:

f_ctm - średnia wytrzymałość betonu na rozciąganie,

f_ctk,0,05 - charakterystyczna wytrzymałość betonu na rozciąganie

(kwantyl 5%)

f_ctk,0,95 - charakterystyczna wytrzymałość betonu na rozciąganie

(kwantyl 95%)

Powyższe trzy rodzaje wytrzymałości betonu na rozciąganie stosuje się odpowiednio do rodzaju rozważanego problemu.

Wytrzymałość obliczeniowa betonu na rozciąganie f_ctd określana jest wzorem

α_ct = 1,0 γ_C = 1,4

ZMIENNOŚĆ WYTRZYMAŁOŚĆI W CZASIE

Wytrzymałość betonu z upływem czasu ulega wzrostowi w wyniku postępującego procesu twardnienia.

Tempo przyrostu wytrzymałości zależy od wielu czynników, z których największy wpływ mają:

• rodzaj i ilość cementu na 1 m³ mieszanki,

• warunki cieplno- wilgotnościowe.

W okresie początkowym przyrost wytrzymałości jest bardzo szybki a po 28 dniach staje się coraz wolniejszy.

Wzrost wytrzymałości betonu nieobciążonego może po 1 roku wynosić 30-75% wytrzymałości 28-dniowej.

W zależności od warunków dojrzewania i pielęgnacji beton może nie wykazywać wzrostu wytrzymałości.

W obliczeniach konstrukcji przyjmuje się zawsze 28-dniową wytrzymałość betonu.

ZALEŻNOŚĆ NAPRĘŻENIE - ODKSZTAŁCENIE

Wykres zależności σ_c- ε_c określa się na podstawie badań walcowych próbek betonowych ściskanych osiowo aż do zniszczenia.

Badania takie wykonuje się sporadycznie.

Do projektowania przekrojów korzystamy z następujących zależności σ_c-ε_c podanych w EC2:

Rysunek 3.3: Wykres parabola - prostokąt

Rysunek 3.4: Wykres bilinearny

ε_c2 - najmniejsze odkształcenie, przy którym osiąga się

wytrzymałość betonu, dla f_ck ≤ 50 MPa ε_c2 = 2 ‰

ε_cu2 - odkształcenie graniczne (ultimate strain) betonu,

dla f_ck ≤ 50 MPa ε_cu2 = 3,5 ‰

ε_c3 - najmniejsze odkształcenie, przy którym osiąga się

wytrzymałość betonu, dla f_ck ≤ 50 MPa ε_c3 = 1,75 ‰

ε_cu3 - odkształcenie graniczne (ultimate strain) betonu,

dla f_ck ≤ 50 MPa ε_cu3 = 3,5 ‰

Wszystkie wartości odkształceń podane są w Tabl. 3.1

Podstawowym założeniem jest przyjęcie, że dla klas betonów zwykłych (C12/15 do C50/60) wartości odkształceń granicznych są stałe i nie zależą od klasy betonu.

MODUŁ SPRĘŻYSTOŚCI BETONU

Wartości modułu sprężystości E_c betonu określa się ze znanego warunku:

E_c= σ_c / ε_c

Praktyczne znaczenie ma tzw. średni moduł sprężystości E_cm, którego wartości są podane w normie.

Np. wg tabl. 3.1 dla C25/30 E_cm = 31 GPa

Wartość modułu sprężystości zależy od klasy betonu

SKURCZ BETONU

Dojrzewanie i twardnienie świeżego betonu w warunkach suchych powoduje zmniejszenie jego objętości zwane skurczem.

Jeżeli proces twardnienia betonu przebiega w wodzie, to występuje zjawisko odwrotne, zwane pęcznieniem.

Wartości skurczu i pęcznienia zależą od wieku i składu betonu, warunków cieplno-wilgotnościowych oraz wymiarów elementu.

Roczny skurcz betonu wynosi zwykle 0,2-0,5 mm/m,

w zaprawach cementowych dochodzi do 2 mm/m.

Skurcz ustaje z upływem czasu osiągając po około 3 latach końcową wartość odkształceń skurczowych.

Zgodnie z EC2 wartość całkowitego odkształcenia skurczowego ε_cs określa się wzorem:

ε_cs = ε_cd + ε_ca

ε_cd - odkształcenia skurczowe spowodowane wysychaniem

ε_ca - odkształcenia skurczu autogenicznego (samorodnego)

Wartości wymienionych odkształceń skurczowych można wyliczyć z zależności podanych w EC2 p. 3.1.4

PEŁZANIE BETONU

Pełzanie betonu jest to przyrost odkształceń elementu pod działaniem długotrwałych stałych obciążeń.

Odkształcenia wywołane pełzaniem zależą od wielu czynników:

wieku betonu w chwili obciążenia

poziomu naprężeń ściskających w betonie σ_c

wilgotności względnej powietrza i wymiarów elementu

Proces pełzania może trwać wiele lat, z czasem maleje i zanika.

Pełzanie betonu może być opisane za pomocą współczynnika pełzania φ(∞, t₀).

Jeżeli w obliczeniach nie jest wymagana duża dokładność, współczynnik ten można odczytać z wykresów podanych w EC2 na rys. 3.1.

Musi być jednak spełniony warunek, że przy pierwszym obciążeniu w wieku t₀ beton nie został poddany naprężeniu ściskającemu większemu niż 0,45 f_ck.

Odkształcenia pełzania ε_cc(∞, t₀) po czasie t = ∞ przy stałym naprężeniu ściskającycm σ_c w oblicza się ze wzoru:

ε_cc(∞, t₀) = φ(∞, t₀)

Pełzanie ma duży wpływ na ostateczne deformacje elementów z betonu. Wraz z upływem czasu następuje przyrost ugięć, szerokości rozwarcia rys oraz wzrost strat siły sprężającej w konstrukcjach sprężonych. Efekty spowodowane zjawiskiem pełzania betonu muszą być uwzględniane w obliczeniach konstrukcji.

WSPÓŁCZYNNIK LINIOWEJ ROZSZERZALNOŚCI TERMICZNEJ

Wartość współczynnika liniowej rozszerzalności termicznej betonu można przyjmować:

α_t = 1 x 10 ^-5 / ⁰C

W przedziale najczęściej spotykanych temperatur, tj.

od -20⁰C do +100⁰C, wartość ta nie odbiega od termicznej odkształcalności stali (1,2 x 10 ^-5 / ⁰C).

STAL ZBROJENIOWA wg EC2

Informacje podane w EC2 w rozdz. 3.2 dotyczą ogólnych właściwości stali zbrojeniowej.

W tekście EC2 występują liczne odwołania do PN-EN 10080 „Stal do zbrojenia betonu” oraz innych norm i przepisów.

Zakres stosowania EC2 odnosi się wyłącznie do zbrojenia żebrowanego, które spełnia wymagania zawarte w Załączniku C.

Należy zaznaczyć, że Załącznik C dopuszcza przedział f_yk między 400 a 600 MPa.

Podział na klasy stali A, B, C podany w Załączniku C zależy od ciągliwości.

Zgodnie z klasyfikacją podaną w EC2 w normie PN-B-03264 nie ma najbardziej ciągliwej stali klasy C.

Stal A-IIIN należy do klasy A, stale A-0÷A-III do klasy B.

Obliczeniowa granica plastyczności zbrojenia f_yd

f_yk - charakterystyczna granica plastyczności

γ_S - częściowy współczynnik dla stali (patrz EC2 tab. 2.1N)

w sytuacjach trwałych i przejściowych γ_S = 1,15.

Tak więc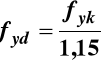

Obecnie najczęściej stosowaną stalą zbrojeniową jest stal klasy C,

której f_yk wynosi 400 do 600 MPa.

Charakterystyczna granica plastyczności np. dla popularnej stali B500SP, klasy C wynosi f_yk = 500 MPa

ZALEŻNOŚĆ NAPRĘŻENIE - ODKSZTAŁCENIE

Norma EC2 podaje alternatywne zależności naprężenie-odkształcenie dla stali zbrojeniowej (górna gałąź wykresu jest prosta lub pochylona, patrz rys. 3.8).

Norma EC2 dopuszcza przyjmowanie do obliczeń wykresu σ-ε stali w postaci uproszczonej z poziomą półką, przy czym nie ma potrzeby sprawdzania ograniczeń odkształcenia.

Rys. 3.8 Wykresy (wyidealizowany i obliczeniowy) naprężenie-odkształcenie stali zbrojeniowej (ściskanie i rozciąganie)

ε_ud - obliczeniowe odkształcenie stali przy

maksymalnym obciążeniu, przy czym ε_ud = 0,9 ε_uk

ε_uk - charakterystyczne odkształcenie stali przy max. obc.

k = (f_t/f_y)_k - parametr ciągliwości, patrz Załącznik C

Przy projektowaniu elementów można przyjmować, że obliczeniowa wartość modułu sprężystości wynosi E_s = 200 GPa.

STAL ZBROJENIOWA wg PN-B-03264

Informacje o stalach zbrojeniowych produkowanych w Polsce zawarte są w normie budowlanej PN-B-03264 oraz normie hutniczej PN-H-93215.

Wyroby budowlane (w tym także stale ), których właściwości nie odpowiadają normom to mogą być stosowane pod warunkiem, że posiadają aktualną aprobatę techniczną.

Zgodnie z normą PN-B-03264 wyróżnia się 5 klas stali:

A-O, A-I, A-II, A-III, A-IIIN.

Klasa stali to określenie własności mechanicznych

stali zbrojeniowych.

Pręty ze stali klasy A-0 i A-I są gładkie i wymagają na ogół zakończeń hakowych ( dla zwiększenia przyczepności w strefie zakotwienia).

Pręty klasy A-II, A-III, A-IIIN są żebrowane, mają dobrą przyczepność do betonu i można je stosować bez zakończeń hakowych.

Klasie stali przypisane są :

• znak gatunku stali,

• nominalna średnica prętów Φ [mm],

• charakterystyczna granica plastyczności f_yk,

• obliczeniowa granica plastyczności f_yd,

• wytrzymałość charakterystyczna na zerwanie f_tk.

Wartości f_yk, f_yd, f_tk podane są w tablicy 3 w normie PN-B.

Stale żebrowane mają zróżnicowany układ żeberek, ułatwia to rozpoznanie poszczególnych gatunków stali.

Pręty ze stali klasy A-II żebrowane są spiralnie (rys a,b),

natomiast klasy A-III i A-IIIN w jodełkę (rys c,d).

Rysunek2.15 str 84 Łapko

Stale żebrowane

a) A-II gatunek 18G2 b) A-II gatunek St50B

c)A-III gatunek 34GS d) A-IIIN gatunek 20G2VY

Zgodnie z wytycznymi Instytutu Techniki Budowlanej podstawowym gatunkiem stali do wykonywania zbrojenia nośnego konstrukcji jest stal klasy A-III, gatunek 34G S.

Stal ta nie może być stosowana w elementach obciążonych dynamicznie, dopuszcza się stosowanie w przypadku obciążeń wielokrotnie zmiennych.

W krajach Unii Europejskiej powszechnie stosowana jest stal żebrowana gatunku B500, która ma granicę plastyczności powyżej 500 MPa.

Polskie huty produkują także stal o podwyższonej wytrzymałości gatunku RB500W oraz BSt500S i posiadają dla tych wyrobów odpowiednie aprobaty techniczne.

RODZAJE ZBROJENIA

Zbrojenie konstrukcji żelbetowych w zależności od pełnionej funkcji dzieli się na:

• nośne ,

• montażowe,

• rozdzielcze.

Przekrój zbrojenia nośnego, nazywanego też głównym lub konstrukcyjnym określa się na podstawie obliczeń.

Przekrój zbrojenia montażowego i rozdzielczego nie jest obliczany, lecz przyjmowany na podstawie warunków normowych.

Zbrojenie dostarczane jest na budowę w kręgach (małe średnice) oraz w postaci prętów prostych o długości do 12m. Większe długości można otrzymać tylko w uzgodnieniu z producentem.

KSZTAŁT ZBROJENIA

Pręty proste

Pręty rozciągane gładkie (klasy A-0, A-I) można kończyć hakiem półokrąglym, pręty żebrowane (klasy A-II, A-III, A-IIIN) kończy się bez haka, hakiem prostym lub pętlą.

Pręty ściskane, niezależnie od klasy stali kończy się bez haka.

Siatki zbrojeniowe

a) płaska b) zwinięta w rulon

Szkielety zbrojeniowe

FAZY NAPRĘŻEŃ W BELCE ZGINANEJ

Rozpatrzmy zachowanie się żelbetowej belki jednoprzęsłowej, swobodnie podpartej, obciążonej siłą skupioną (pomijamy wpływ ścinania).

W belce poddanej działaniu momentu zginającego powstają naprężenia normalne pochodzące od zginania:

• naprężenia ściskające - powyżej osi obojętnej,

• naprężenia rozciągające - poniżej osi w tzw. strefie rozciąganej.

Analizując poszczególne przekroje belki zauważamy, że naprężenia w nich występujące wzrastają proporcjonalnie ze wzrostem momentu.

Na długości belki obserwujemy różne rozkłady naprężeń zwane potocznie fazami wytężenia elementu żelbetowego:

• w fazie I pracują przekroje niezarysowane,

• faza II obejmuje przekroje zarysowane,

• faza III odpowiada stadium osiągnięcia nośności.

faza Ia

Wartość momentu jest niewielka.

Wykres naprężeń jest liniowy na całej wysokości przekroju.

faza Ib

Wartość momentu wzrasta.

Wykres naprężeń w strefie ściskanej jest nadal prostoliniowy.

Nastąpiło uplastycznienie betonu strefy rozciąganej (wykres naprężeń krzywoliniowy).

Faza tuż przed pojawieniem się rysy.

Na rysunku można zauważyć, że w przekrojach między rysami belka zachowuje się jak w fazie I. Oznacza to, że beton rozciągany nadal współpracuje tam ze zbrojeniem.

faza IIa

Po zarysowaniu betonu całość sił rozciągających przejmuje zbrojenie.

W strefie ściskanej rozkład naprężeń w betonie jest nadal prostoliniowy.

faza IIb

Zasięg rys jest coraz większy.

Wykres naprężeń na wysokości strefy ściskanej jest wyraźnie krzywoliniowy.

faza III

Faza zniszczenia (wyczerpania nośności)

Zniszczenie może nastąpić w wyniku

wyczerpania nośności strefy ściskanej

(ang. compression failure)

Naprężenie w betonie jest równe jego wytrzymałości na ściskanie.

Zniszczeniu może ulec strefa rozciągana - gdy naprężenie w zbrojeniu osiągnie granicę plastyczności

(ang. tension failure).

Zachowanie się przekroju w fazie III i związany z nią rozkład naprężeń jest podstawą do wymiarowania elementów w stanie granicznym nośności.

WYTRZYMAŁOŚĆ BETONU NA ŚCISKANIE

Za podstawę oceny jakości betonu przyjęto jego wytrzymałość na ściskanie.

Podstawową wytrzymałością betonu na ściskanie f_c jest

wytrzymałość charakterystyczna f_ck.

Wyznaczona zgodnie z normą PN-EN 206-1 na próbkach walcowych 150/300 mm po 28 dniach od wykonania, oznaczona jest symbolem f_ck,cyl.

Norma PN-EN 206-1 wymienia również wytrzymałość charakterystyczną kostkową f_ck,cube badaną na kostkach o boku 150 mm.

Wytrzymałość charakterystyczna jest definiowana jako dolny 5% kwantyl statystycznego rozkładu wytrzymałości.

(Kwantyl 5% oznacza, że np. ze 100 badanych próbek tylko 5 może mieć wytrzymałość mniejszą niż f_ck.)

Podstawą określenia klasy betonu jest jego wytrzymałość charakterystyczna na ściskanie.

PN-EN 206-1, Tablica 7- Klasy wytrzymałości na ściskanie betonu zwykłego i betonu ciężkiego

Klasa wytrzym. na ściskanie	Minimalna wytrzym. charakterystyczna oznaczna na próbkach walcowych fck,cyl N/mm^2	Minimalna wytrzym. charakterystyczna oznaczna na próbkach sześciennych fck,cube N/mm^2
C8/10 C12/15 C16/20 C20/25 C25/30 C30/37 C35/40 C40/50 C45/55 C50/60	8 12 16 20 25 30 35 40 45 50	10 15 20 25 30 37 40 50 55 60

Klasa betonu = minimalna wytrzymałość charakterystyczna oznaczana na walcach lub kostkach

Normy PN-EN 1992-1-1 oraz EC 2 stosują analogiczne

oznaczenie klasy betonu.

C fck/fck,cube np. C 20/25

(Uwaga: w powyższych normach charakterystyczną wytrzymałość walcową oznaczono skrótowo jako f_ck )

Wszystkie informacje o betonie podane są w PN-EN 1992-1-1,

w tablicy 3.1, w której wyszczególnione są następujące wytrzymałości: f_ck, f_ck,cube, f_cm, f_ctm, f_ctk,0,05, f_ctk,0,95 oraz podane odpowiednie wzory przeliczeniowe.

Omówione wytrzymałości charakterystyczne używane są

gdy projektujemy konstrukcję w stanach granicznych użytkowalności SGU.

W normie żelbetowej PN-B-03264 stosowane było oznaczenie symbolem np. B20, które oznacza, że jest to beton klasy 20

o wytrzymałości gwarantowanej równej 20 MPa.

Norma ta wprowadziła poprawkę, która uwzględnia nowe oznaczenia klas betonu, jakie znalazły się w normie PN-EN 206-1.

Poprawkę tą stanowi załącznik F.

Załącznik F (informacyjny) RÓWNOWAŻNE OZNACZENIA KLAS BETONU LITERAMI B (podane w PN-88/B-06250) i C (podane w PN-EN 206-1:2003) Tablica F.1 - Równoważne oznaczenia klas betonu B15 B20 B25 B30 B37 B45 B50 B55 B60 C12/15 C16/20 C20/25 C25/30 C30/37 C35/45 C40/50 C45/55 C50/60

W normie PN-B-03264 wszystkie informacje o betonie podane są

w Tablicy 2 - Wytrzymałości i moduł sprężystości betonu przyjmowane do obliczeń.

Wytrzymałość obliczeniowa betonu na ściskanie f_cd

używana w obliczeniach stanów granicznych nośności SGN.

Określana jest ze wzoru

α_cc - współczynnik, którego wartość zalecana w Załączniku

krajowym α_cc = 1,0

(wg EC2 może być przyjmowana w przedziale 0,8 do 1,0)

γ_C - częściowy współczynnik dla betonu, którego wartość w

Załączniku krajowym w tab. NA.2 przyjęto γ_C = 1,4

(wg EC2 tab. 2.1N, przyjęto w sytuacjach trwałych i

przejściowych γ_C = 1,5 )

Tak więc

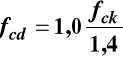
czyli

WYTRZYMAŁOŚĆ BETONU NA ROZCIĄGANIE f_ct

Wartość wytrzymałości betonu na rozciąganie zależy od klasy betonu, a więc od wytrzymałości na ściskanie.

Wytrzymałość betonu na rozciąganie wynosi około 10% jego wytrzymałości na ściskanie

Wytrzymałość betonu na rozciąganie f_ct odpowiada maksymalnemu naprężeniu, jakie może przenieść beton pod obciążeniem osiowym.

Tablica 3.1 w PN-EN 1992-1-1 podaje następujące wartości:

f_ctm - średnia wytrzymałość betonu na rozciąganie,

f_ctk,0,05 - charakterystyczna wytrzymałość betonu na rozciąganie

(kwantyl 5%)

f_ctk,0,95 - charakterystyczna wytrzymałość betonu na rozciąganie

(kwantyl 95%)

Powyższe trzy rodzaje wytrzymałości betonu na rozciąganie stosuje się odpowiednio do rodzaju rozważanego problemu.

Wytrzymałość obliczeniowa betonu na rozciąganie f_ctd określana jest wzorem

α_ct = 1,0 γ_C = 1,4

Tak więc

Uwaga!

W normie PN-B- 03264 oraz EC2 przyjęto γ_C = 1,5,

dlatego odpowiednie wartośći f_cd oraz f_ctd tam podawane różnią się od wartości przyjmowanych w PN-EN 1992-1-1.

STAL ZBROJENIOWA wg EC2

Informacje podane w EC2 w rozdz. 3.2 dotyczą ogólnych właściwości stali zbrojeniowej.

W tekście EC2 występują liczne odwołania do PN-EN 10080 „Stal do zbrojenia betonu” oraz innych norm i przepisów.

Zakres stosowania EC2 odnosi się wyłącznie do zbrojenia żebrowanego, które spełnia wymagania zawarte w Załączniku C.

Należy zaznaczyć, że Załącznik C dopuszcza przedział f_yk między 400 a 600 MPa.

Podział na klasy stali A, B, C podany w Załączniku C zależy od ciągliwości.

Zgodnie z klasyfikacją podaną w EC2 w normie PN-B-03264 nie ma najbardziej ciągliwej stali klasy C.

Stal A-IIIN należy do klasy A, stale A-0÷A-III do klasy B.

Obliczeniowa granica plastyczności zbrojenia f_yd

f_yk - charakterystyczna granica plastyczności

γ_S - częściowy współczynnik dla stali (patrz EC2 tab. 2.1N)

w sytuacjach trwałych i przejściowych γ_S = 1,15.

Tak więc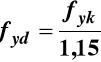
czyli

Obecnie najczęściej stosowaną stalą zbrojeniową jest stal klasy C,

której f_yk wynosi 400 do 600 MPa.

Charakterystyczna granica plastyczności np. dla stali B500SP,

klasy C wynosi f_yk = 500 MPa

Można więc określić obliczeniową wartość odkształcenia plastycznego w zbrojeniu wykonanym z takiej stali.

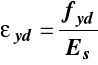
gdzie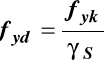
więc

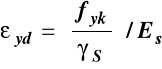
dla: f_yk = 500 MPa γ_S = 1,15 E_s = 200 GPa

ε_yd = 500/(1,15 ∙ 200 ∙ 10³)

ε_yd = 0,00217

ELEMENTY ZGINANE

Ustroje prętowe, płytowe lub tarczowe, którymi w praktyce są belki oraz płyty to typowe przykłady elementów zginanych.

W żelbetowych elementach zginanych, po przekroczeniu naprężeń w strefie rozciąganej, pojawią się rysy prostopadłe do osi elementu.

Mogą też pojawić się rysy ukośne na odcinkach przy podporach lub w okolicy przyłożenia siły skupionej.

W związku z tym obliczanie nośności elementów zginanych - zwłaszcza belek przeprowadza się w dwóch etapach:

• na zginanie, czyli oddziałanie momentów zginających,

• na ścinanie, czyli oddziaływanie sił poprzecznych

(omówione w dalszym rozdziale).

Żelbetowa belka wolnopodparta, równomiernie obciążona:

• obraz zarysowania,

• wykres momentów zginających i sił poprzecznych.

Uwzględniając zbrojenie konstrukcyjne

oraz różnego rodzaju zbrojenie pomocnicze

ilość stali nie przekracza na ogół 5 %

---