Grupa.4.

Sprawozdanie:

Ćwiczenie 55

Badanie czasowego przebiegu ładowania kondensatora.

Wstęp:

Celem mojego ćwiczenia jest zbadanie i opis procesu ładowania i rozładowywania kondensatora, gdy upływność praktycznie nie występuje(przypadek1) i gdy należy ją uwzględnić(przypadek2).

Wykonanie zadania:

1.Ładowanie kondensatora.

1. Łączymy obwód wg. Rys.1(Z-zasilacz wysokiego napięcia)

Rys.1

.

b. Przy zamkniętym wyłączniku W ustawiamy napięcie pracy tak, aby wskazania mikroamperomierza były bliskie maksymalnej dopuszczalnej wartości.

c. Włączając stoper jednocześnie z otwarciem włącznika W, ładujemy kondensator; mierzymy czasy, po których natężenie prądu spada od Io do coraz to mniejszych wartości I.

d. Sporządzamy wykres I=f(t) i zaznaczamy błędy bezwzględne ΔI (z klasy przyrządu) i Δt (dokładność stopera) dla poszczególnych pomiarów. Z wykresu Rys.2 odczytujemy stałą czasową obwodu τ1, a także wartość błędu bezwzględnego Δτ1 stałej czasowej.

Rys.2

e. Obliczamy teoretyczną wartość stałej czasowej τ=RC; C oznacza pojemność baterii kondensatorów.

f. Porównujemy wyniki odczytane z wykresu i obliczone.

2.Ładowanie kondensatora z upływnością i wyznaczanie oporu dielektryka.

g. Łączymy obwód jak w części 1, ale podłączamy tylko jeden kondensator.

h. Mierzymy zależność prądu ładowania od czasu.

1. Obliczamy wartość oporu dielektryka z zależności r =
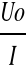
   -R .Uo odczytujemy na zasilaczu, I na mikroamperomierzu po ustaleniu się wartości ładowania.

j. Sporządzamy wykres I =f(t). Obliczamy I1 ze wzoru

I1 =

i odczytujemy z wykresu stałą czasową obwodu τ′1.

k. Obliczamy τ =RC i τ′ ze wzoru Io =

l. Porównujemy otrzymane wyniki.

Obliczenia:

Ad.1.

t[s]	7,5	11	17	22	30	39	51	67	94	215
I[mA]	50	45	40	35	30	25	20	15	10	5

C =8,3mF;Uo =329,5;R =5MΩ; Io =58,5; τ =RC41,5s;

Ad.2.

T[s]	12	27	44	67	100	157	270
I[mA]	50	45	40	35	30	25	20	15	10	5

C =
mF; Uo =329,5; R =5MΩ; Io=55; τ =RC
s

=
+
+

Szeregowe łaczenie kondensatorów

=
+
+

=
mF

C =
mF

C =8
mF

C =8,3mF

R-5MΩ

C-3⋅25mF

Obliczamy teoretyczną wartość stałej czasowej

τ =5MΩ⋅8,3mF =5⋅10⋅8,3⋅10 =5⋅8,3Ω⋅F =41,5s

[Ω⋅F =
⋅
=
=
=s]

Vo = w obu tabelach 329,5V

Jo =w pierwszej tabeli 58,5A

Io =w drugiej tabeli 55A

1 wykres 3 kondensatory

2 wykres 1 kondensator

---