Wykład 31
Polaryzacja
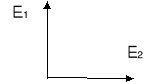
Teoria przewiduje, że światło podobnie jak każda fala elektromagnetyczna jest falą poprzeczną. Kierunki drgań wektorów E i B są prostopadłe do kierunku rozchodzenia się fali. Na rysunku poniżej przedstawione falę elektromagnetyczną, która ma jeszcze dodatkowo pewną charakterystyczną własność:
wektory E są do siebie równoległe we wszystkich punktach fali. Podobnie wektory B.
Mówimy, że ta fala jest płasko spolaryzowana (spolaryzowana liniowo).
Drgający wektor E tworzy z kierunkiem ruchu fali płaszczyznę zwaną płaszczyzną drgań.
W fali spolaryzowanej liniowo wszystkie takie płaszczyzny są równoległe.
Z dotychczas opisanych doświadczeń z interferencją i dyfrakcją nie można wydedukować poprzecznej natury fal świetlnych ponieważ fale podłużne też interferują i ulegają dyfrakcji.
Podstawy doświadczalne przyniosło następujące doświadczenie.
W wyniku oświetlenia kryształu kalcytu (CaCO3) z wiązki padającej można uzyskać dwie oddzielne wiązki (omówione w dalszej części wykładu).
Wiązki te chociaż oczywiście są spójne nie dają prążków interferencyjnych ale równomierne oświetlenie ekranu.
Young wywnioskował z tego faktu, że światło jest falą poprzeczną i że płaszczyzny drgań w tych falach są prostopadłe względem siebie.
Zauważmy, że chcemy dodać dwa zaburzenia falowe takie jak w doświadczeniu Younga tj. ale prostopadłe do siebie. Można udowodnić, że fale świetlne spolaryzowane liniowo o równych amplitudach i prostopadłych kierunkach drgań nie interferują ze sobą dając jednakowe (niezależnie od różnicy faz) natężenie światła na ekranie. Tu tylko zauważmy, że te dwie fale nigdy się nie wygaszają.
W fali poprzecznej, spolaryzowanej liniowo, należy określić dwa kierunki:
kierunek drgania (np. wektora E),
kierunek rozchodzenia się fali.
(Zauważmy, że w fali podłużnej te dwa kierunki się pokrywają.)
Przykładem fal spolaryzowanych liniowo są fale elektromagnetyczne radiowe (oraz mikrofale) emitowane przez antenę dipolową.
W antenie takiej fale wytwarzane są przez ładunek elektryczny drgający w górę i w dół anteny. Taka fala w dużej odległości od dipola, na osi prostopadłej, ma wektor pola elektrycznego równoległy do osi dipola (anteny) jest więc spolaryzowana liniowo. Kiedy taka fala pada na drugi dipol wówczas zmienne pole elektryczne (zmienny wektor E fali) wywołuje w antenie odbiorczej drgania elektronów do góry i w dół (prąd zmienny). Jeżeli jednak obrócimy antenę o 90° wokół kierunku padania fali, to wektor E będzie prostopadły do anteny i nie wywoła ruchu elektronów (antena nie odbiera sygnału).
Źródła światła widzialnego różnią się od źródeł fal radiowych i mikrofal min. tym, że atomy (cząsteczki) emitujące światło działają niezależnie.
W konsekwencji światło rozchodzące się w danym kierunku składa się z niezależnych ciągów fal, których płaszczyzny drgań zorientowane są przypadkowo wokół kierunku ruchu fali (rysunek poniżej). Takie światło chociaż jest falą poprzeczną jest niespolaryzowane.
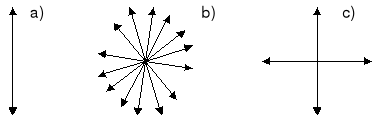
Rysunek poniżej pokazuje różnicę między falą poprzeczną spolaryzowaną liniowo (a) i falą poprzeczną niespolaryzowaną (b). Rysunek (c) przedstawia inny równoważny opis niespolaryzowanej fali poprzecznej; tutaj traktujemy ją jako złożenie dwóch spolaryzowanych liniowo fal o przypadkowo zmiennej różnicy faz. Orientacja kierunków drgań pól E względem kierunku rozchodzenia się fali jest też przypadkowa (ale prostopadła).
Dla zbadania fal świetlnych niespolaryzowanych potrzeba znaleźć metodę, która pozwoliłaby rozdzielić fale o różnych płaszczyznach drgań.
Płytki polaryzujące
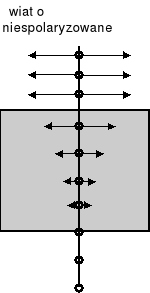
Na rysunku (na następnej stronie) światło niespolaryzowane pada na płytkę z materiału polaryzującego, zwanego polaroidem.
W płytce istnieje pewien charakterystyczny kierunek polaryzacji zaznaczony liniami równoległymi. Płytka przepuszcza tylko te fale, dla których kierunki drgań wektora elektrycznego są równoległe do kierunku polaryzacji, a pochłania te fale, w których są one prostopadłe.
Kierunek polaryzacji ustala się w procesie produkcji:
cząsteczki o strukturze łańcuchowej osadza się na elastycznej warstwie plastycznej,
warstwę rozciąga się co powoduje równoległe ułożenie cząsteczek.
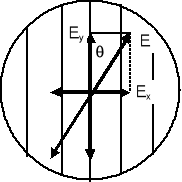
Żeby zanalizować natężenie światła przechodzącego przez polaryzator rozpatrzmy ciąg fal padający na polaroid tak, że wektor E wyznaczający płaszczyznę drgań tworzy kąt θ z kierunkiem polaryzacji płytki (rysunek obok).
Ten ciąg fal jest równoważny ciągom fal o składowych Ex i Ey (składowe wektora E).
Składowa równoległa Ey = Ecosθ jest przepuszczana podczas gdy składowa prostopadła Ex = Esinθ jest pochłaniana.
Postawmy teraz na drodze światła drugą płytkę polaryzującą (tak zastosowaną płytkę nazywamy analizatorem). Jeżeli płytkę drugą (analizator) będziemy obracać wokół kierunku padania światła to natężenie światła przechodzącego przez obie płytki będzie się zmieniać osiągając minimum dla położeń różniących się o 180° tj. przy prostopadłych kierunkach polaryzacji obu płytek.
Jeżeli amplituda pola elektrycznego fali padającej na analizator jest równa Em to amplituda fali wychodzącej z analizatora wynosi Emcosθ, gdzie θ jest kątem pomiędzy kierunkami polaryzacji obu płytek. Ponieważ natężenie światła jest proporcjonalne do kwadratu amplitudy więc otrzymujemy
I = Imcos2θ |
(30.1) |
Zauważmy, że I ma maksimum dla θ = 0° lub θ = 180° a minimum dla θ = 90° lub θ = 270°.
Powyższe równanie zwane jest prawem Malusa.
Znane są jeszcze inne sposoby otrzymywania światła spolaryzowanego. Niektóre omówione są poniżej.
Polaryzacja przez odbicie
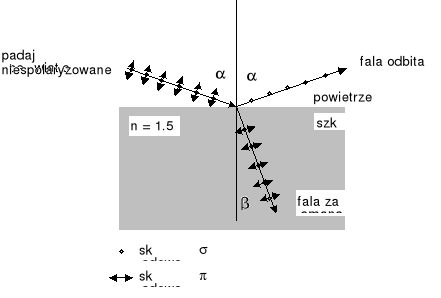
W 1809 r. Malus odkrył, że światło może być częściowo lub całkowicie spolaryzowane przez odbicie. Rysunek przedstawia wiązkę niespolaryzowaną padającą na powierzchnię szkła. Wektor E można rozłożyć na dwie składowe:
składową σ prostopadłą do płaszczyzny padania (płaszczyzna rysunku),
składową π leżącą w płaszczyźnie padania.
Dla światła całkowicie niespolaryzowanego obie składowe maja jednakowe amplitudy.
Stwierdzono doświadczalnie, że dla szkła (i innych materiałów dielektrycznych) istnieje pewien kąt padania, nazywany kątem całkowitej polaryzacji αp, dla którego współczynnik odbicia składowej π jest równy zero. Wtedy wiązka odbita jest spolaryzowana liniowo prostopadle do płaszczyzny padania. Wiązka przechodząca jest tylko częściowo spolaryzowana (składowa π jest całkowicie załamana, a składowa σ tylko częściowo). Zwróćmy uwagę, że wiązka załamana ma większe natężenie od wiązki odbitej.
Doświadczalnie stwierdzono, że gdy kąt padania jest równy kątowi całkowitej polaryzacji to wówczas wiązka odbita i załamana tworzą kąt prosty co oznacza że
α + β = 90°
Natomiast z prawa załamania mamy
![]()
Z obu tych równań otrzymujemy
![]()
albo
|
(30.2) |
przy czym promień pada z ośrodka 1 i załamuje się w ośrodku 2.
To ostatnie równanie jest nazywane prawem Brewstera.
Prawo to zostało znalezione doświadczalnie ale oczywiście można je wyprowadzić ściśle przy pomocy równań Maxwella.
Załamanie podwójne
Dotychczas milcząco zakładaliśmy, że prędkość światła, a więc i współczynnik załamania, nie zależą od kierunku rozchodzenia się światła w ośrodku ani od jego polaryzacji. Ciała spełniające te warunki nazywamy ciałami optycznie izotropowymi. Istnieje jednak szereg ciał anizotropowych (nie izotropowych).
Dotyczy to nie tylko własności optycznych ale wielu innych. Np. pewne kryształy łamią się łatwo tylko w jednej płaszczyźnie, opór elektryczny mierzony w różnych kierunkach jest różny. Kryształy łatwiej magnesuje się w jednym kierunku niż innych itd.
Uwaga: Ciała polikrystaliczne (złożone z wielu małych kryształków) z powodu przypadkowej orientacji kryształków mogą wydawać się izotropowymi.
Na początku wykładu wspomniany został eksperyment z kryształem kalcytu.
Na rysunku poniżej niespolaryzowana wiązka światła pada na kryształ kalcytu prostopadle do jednej z jego ścian.
Pojedyncza wiązka rozszczepia się na powierzchni kryształu na dwie.
Mamy do czynienia z podwójnym załamaniem.
Możemy zanalizować obie wychodzące wiązki za pomocą płytki polaryzującej.
Okazuje się, że obie wiązki są spolaryzowane liniowo, przy czym ich płaszczyzny drgań są wzajemnie prostopadłe. Wiązki te są oznaczone przez o i e.
Jeżeli zmienimy kąt padania to okaże się, że jedna z wiązek tzw. promień zwyczajny o spełnia prawo załamania (tak jak dla ośrodka izotropowego) a druga wiązka tzw. promień nadzwyczajny e nie spełnia tego prawa.
Na rysunku kąt padania jest równy zeru więc i kąt załamania też powinien być zerowy i tak jest dla promienia o ale nie dla promienia e.
Różnicę tę można wyjaśnić następująco:
promień o przechodzi przez kryształ z jednakową prędkością we wszystkich kierunkach tzn. ma jeden współczynnik załamania n0 tak jak izotropowe ciało stałe.
promień e ma prędkość w krysztale zależna od kierunku tzn. prędkość zmienia się od v0 do ve a współczynnik załamania od no do ne. Dla kalcytu ne = 1.658, no = 1.486.
Wielkości ne i n0 nazywamy głównymi współczynnikami załamania kryształu.
Niektóre podwójnie załamujące kryształy mają interesującą własność nazywaną dichroizmem, polegającą na tym, że jedna ze składowych polaryzacji jest pochłaniana silniej niż druga. Własność ta jest pokazana na rysunku obok. Na tej zasadzie opiera się działanie szeroko stosowanych polaroidów.
Zamiast dużej płytki wyciętej z kryształu można zastosować wiele małych kryształów o osiach optycznych ustawionych równolegle do siebie.
Niektóre przezroczyste ciała bezpostaciowe jak szkła czy tworzywa sztuczne optycznie izotropowe pod wpływem przyłożonych naprężeń mechanicznych stają się optycznie anizotropowe.
Fakt ten jest szeroko wykorzystywany w technice do badania naprężeń w różnych konstrukcjach i mechanizmach.
Naprężenia można wyznaczyć ilościowo, budując model plastyczny urządzenia, które poddaje się działaniu różnych sił. Anizotropię optyczną, jaka przy tym powstaje w modelu, bada się przy pomocy polaryzacji.
Z. Kąkol-Notatki do Wykładu z Fizyki
25-8
31-6
Wyszukiwarka
Podobne podstrony:
wykład 8-31.05, WSA, prawo administarcyjne z prawem wspólnot samorządowych, wykłady, sem 2
PATOMORFOLOGIA wykład 31 5, PATOMORFOLOGIA wykład 5 (9 XI 01)
(Komentarz do wykładu 31 1 6)
Wykład 31
Wykład 31
NOWOTWORY wykład 31 01 2010
marketing-wykłady D.31.01.2009
miedzynarodowe centra tur. i hotelarskie wyklad 31.10.10, międzynarodowe ośrodki i centra tur.-hot
miedzynarodowe centra tur. i hotelarskie wyklad 31.10.10, międzynarodowe ośrodki i centra tur.-hot
Wykład 5 - 31.03.2011, Notatki UTP - Zarządzanie, Semestr II, Nauka o organizacji
Z Wykład 31.05.2008, Programowanie
(Komentarz do wykładu 31 1-6)
WPROWADZENIE DO PEDAGOGIKI - WYKŁADY (31.09.2006), PEDAGOGIKA
obsluga klienta w turystyce i hotelarstwie wykład 2 31.10.10, GWSH, obsługa klienta w tur. i hot
Psychologia rozwojowa - Brzezińska - wykład 31 - Dziadkowie, Psychologia rozwoju człowieka
Wykład 3 - 31.03.2011, Notatki UTP - Zarządzanie, Semestr II, Zarządzanie zasobami ludzkimi
więcej podobnych podstron