Najlepsza liniowa nieobciążona predykcja (BLUP - best linear unbiased prediction)

Wiadomości ogólne

Podstawową metodą hodowlaną stosowaną w populacjach zwierząt gospodarskich jest selekcja, która polega na wyborze na rodziców zwierząt najlepsze pod względem genetycznym po to, aby uzyskać jak najlepsze potomstwo. Miarą wartości genetycznej jest wartość hodowlana. Aby zatem selekcja mogła być przeprowadzana skutecznie muszą być znane wartości hodowlane selekcjonowanych zwierząt. Wartości hodowlanej nie można zmierzyć bezpośrednio. Możemy ją jednak określić pośrednio na podstawie obserwacji (wydajności) cech samego ocenianego osobnika albo jego krewnych. Ze statystycznego punktu widzenia zagadnienie sprowadza się do określenia jednej zmiennej na podstawie wartości przyjmowanych przez jedną lub kilka innych zmiennych. Gdy zależność między tymi wartościami jest liniowa najlepiej jest użyć równania regresji prostej lub wielokrotnej. Można więc mówić o ocenie wartości hodowlanej na podstawie jednego źródła informacji albo na podstawie wielu (kilku) źródeł informacji. Tymi źródłami informacji mogą być zmierzone wartości cechy (cech) samego ocenianego osobnika, bądź jego krewnych.

BLUP. Model mieszany

Proces przewidywania (prognozowania) wartości zmiennej losowej na podstawie wartości przyjmowanych przez inną zmienną losową (inne zmienne losowe) nazywa się predykcją, natomiast funkcję, na podstawie, której dokonuje się tego przewidywania nazywa się predyktorem. Pojęcia te są analogiczne do pojęć estymacja i estymator, odnoszących się do określania nieznanego parametru populacji.

Niech g oznacza zmienną losową, której wartości nie można obserwować, zaś x wektor obserwacji, na podstawie których chcemy przewidzieć tę wartość, tzn. uzyskać predyktor
. Metodę określania predykatora, dla której wartość oczekiwana kwadratu różnicy g -
jest minimalna, tzn.

E(g - )² = min.

Nazywa się najlepszą predykcją (Best prediction - BP). Powyższy warunek spełnia funkcja regresji

Aby określić funkcję regresji trzeba znać łączny rozkład g oraz x, a gdy nie jest znany, z konieczności należy się ograniczyć do liniowej funkcji regresji, tzn. przyjąć, że

+βx

Gdzie β = [β₁, β₂, …β_p] jest wierszowym wektorem cząstkowych współczynników regresji. Ta metoda przewidywania wartości g nazywa się najlepszą liniową predykcją. Jeżeli łączny rozkład g i x jest normalny, to BLP jest również BP. Do określenia współczynników regresji trzeba znać tylko wariancje zmiennych losowych g i poszczególnych x_i oraz ich kowariancje. Aby uzyskać predyktor
należy znać średnie g oraz x_i.

Gdy wartości średnie g oraz x_i nie są znane, należy je zastąpić ich estymatorami. Dokładność takiej metody będzie zależeć od tego jakie estymatory zostaną użyte. Pożądane jest, aby predykator był nieobciążony, tzn. aby

E(
) - E(g) oraz E(g - )² = min.

Metodę, która umożliwia znalezienie wśród liniowych predykatorów nieobciążonych predykatora z minimalnym średnim kwadratowym błędem, nazywa się najlepszą nieobciążoną liniową predykcją.

Ocena wartości hodowlanej metodą BLUP wymaga rozwiązania układu równań związanego z modelem mieszanym. Poniższy przykład posłuży do zilustrowania konstrukcji macierzy, które w tym układzie występują.

Przyjmijmy, że wydajność osobnika określa model

x_ijk = µ + h_i + s_j + e_ijk

W którym x_ijk oznacza wydajność k-tego potomka j-tego ojca w i-tym stadzie, µ oznacza średnią wydajność populacji, h_i - oznacza efekt i-tego stada, s_j - efekt j-tego ojca, e_ijk - oznacza efekt losowy - specyficzny dla k-tego potomka j-tego ojca z i-tego stada. Liczbę potomków j-tego ojca w i-tym stadzie oznaczamy n_ij. Zakładamy, że µ oraz h_i są efektami stałymi, a s_j zmienną losową. Wobec takich założeń, model ten nazywamy mieszanym. Tabela 1. zawiera dane do rozpatrywanego przykładu (bez wydajności).

Tabela 1.

Ojciec Stado j i	1	2	3	Suma
1 2	n11 = 0 n21=1	n12= 2 n22=0	n13=1 n23=3	n1.=3 n2.=4
Suma	n.1=1	n.2=2	n.3=4	n..=7

Korzystając z danych zawartych w tabeli 1. Możemy napisać równania dla wydajności poszczególnych potomków. Równań musi być 7 - po jednym równaniu dla każdego osobnika

x₁₁₁ = µ + h₁ + s₁ + e₁₁₁ to równanie jest niepotrzebne, bowiem nie ma żadnego potomka pierwszego ojca w pierwszym stadzie

x₁₂₁ = µ + h₁ + s₂ + e₁₂₁ obok zestawiono µ h₁ h₂ s₁ s₂ s₃

x₁₂₂ = µ + h₁ + s₂ + e₁₂₂ współczynniki 1 1 0 0 1 0

x₁₃₁ = µ + h₁ + s₃ + e₁₃₁ przy µ, h, s 1 1 0 0 1 0

x₂₁₁ = µ + h₂ + s₁ + e₂₁₁ 1 1 0 0 0 1

x₂₃₁ = µ + h₂ + s₃ + e₂₃₁ 1 0 1 1 0 0

x₂₃₂ = µ + h₂ + s₃ + e₂₃₂ 1 0 1 0 0 1

x₂₃₃ = µ + h₂ + s₃ + e₂₃₃ 1 0 1 0 0 1

1 0 1 0 0 1

Zielonym kolorem zaznaczono współczynniki przy efektach stałych modelu.

Poniżej zapisano odpowiednie macierze:

X =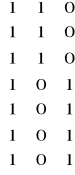
Z =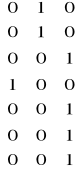
e =
y =

Układ równań można zapisać w symbolice macierzowej jak niżej:

y = X α +Z s + e

Macierz X jest macierzą współczynników przy efektach stałych, wskazuje więc, które efekty są związane z poszczególnymi wydajnościami. Macierz Z jest macierzą związaną z efektami losowymi (macierz współczynników efektów losowych). Macierz e jest wektorem kolumnowym efektów specyficznych (błędu). Macierz Y jest macierzą wydajności (wektor kolumnowy). α jest wektorem kolumnowym efektów stałych [µ h₁ h₂], s jest wektorem kolumnowym efektów losowych [s₁ s₂ s₃].

W tym prostym przykładzie efekty stałe obejmują średnią populacji oraz efekty stad. Można sobie wyobrazić bardziej skomplikowane sytuacje; W przypadku oceny wartości hodowlanej ojców na podstawie potomstwa oceniani ojcowie mogą być podzieleni na grupy między którymi występują systematyczne różnice. Wówczas efekt grupy należy wliczyć do składników stałych modelu.

Należy pamiętać, że średnie dla efektów losowych mają wartości równe zero (efekty ojca s oraz e). Oznaczmy przez G macierz kowariancji dla elementów wektora s, a przez R macierz kowariancji dla wektora e. W większości zastosowań modelu liniowego w hodowli zwierząt przyjmuje się, że e_ijk nie są wzajemnie skorelowane i wariancja każdego e_ijk jest jednakowa i wynosi σ²_e. W zapisie macierzowym oznacza to, że R jest macierzą diagonalną o elementach diagonalnych równych σ²_e, co można zapisać jako:

R = I σ²_e =
σ²_e * R^-1 =

W ogólnym przypadku estymatory
i
wektorów α i s otrzymujemy rozwiązując równanie macierzowe przedstawione po raz pierwszy w pracy C.R. Hendersona Best linear unbised estimation and prediction under a selection model, Biometrics 31, 1975, 423.

**

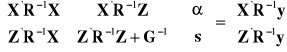
Ponieważ macierz R jest dana wzorem *, to macierz R^-1 ma postać jak obok równania z gwiazdką (*). Wobec czego po pomnożeniu stronami układu równań macierzowych Hendersona otrzymujemy:

***

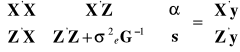
W arkuszu kalkulacyjnym BLUP1.xls wykonano obliczenia iloczynów macierzy z równania Hendersona zamieszczonego powyżej. Warto zauważyć, że wartości otrzymane w wyniku mnożenia odpowiednich macierzy są odpowiednimi liczebnościami.

X^'X =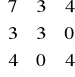
=
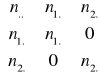
X^'Z =
=

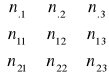
Z^'X = (X^'Z)^' Z^'Z =
=
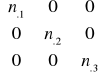
X^'y =
i Z^'y =

Symbol x z kropkami w miejscu wskaźników oznacza sumę obserwacji po tych wskaźnikach, np. x_… jest sumą ogólną obserwacji, x_1.. - sumą obserwacji z pierwszego stada itd.

Ocena wartości hodowlanej metodą BLUP

Aby metodę BLUP zastosować do oceny wartości hodowlanej zwierząt, trzeba poszczególnym składnikom modelu nadać interpretacje genetyczną. Jeżeli oceniane osobniki dzielą się na grupy genetyczne, to różnice między takimi grupami są natury genetycznej. Wówczas wśród efektów stałych reprezentowanych przez wektor α należy wyodrębnić efekty grup genetycznych. W ocenie wartości hodowlanej grupę genetyczną na ogół tworzą buhaje wprowadzone do reprodukcji w tym samym roku. Różnice między grupami z różnych lat odzwierciedlają trend genetyczny, czyli zmianę poziomu genetycznego populacji w czasie. Innym kryterium podziału na grupy jest przynależność do rasy (np. w Polsce).

Poniżej przedstawiono model mieszany z wyodrębnioną grupą genetyczną:

x_ijkl = µ + h_i + a_j + s_jk + e_ijkl

h_i oznacza efekt i=tego stada - jest to czynnik niegenetyczny (może to być również efekt stado-rok-sezon), a_j jest efektem j-tej grupy genetycznej, s_jk oznacza efekt k-tego osobnika (ocenianego) w j-tej grupie genetycznej.

Wartość hodowlaną osobnika definiujemy jako

g_jk = a_j + s_jk

Ocenę wartości hodowlanej metodą BLUP otrzymujemy, zastępując w powyższym wzorze a_j oraz s_jk estymatorami otrzymanymi w wyniku rozwiązania równania Hendersona ***. Ponieważ w ostatnio przywołanym wzorze wartości µ + h_i nie występują, nie muszą być szacowane. Możemy wobec tego zmodyfikować model zastępując µ + h_i przez r_i. otrzymamy zatem model jak niżej:

x_ijkl = r_i + a_j + s_jk + e_ijkl

Modelowi temu odpowiadać będzie macierz X bez pierwszej kolumny (kolumny jedynek) oraz wektor α bez stałej µ. Wektor α i macierz X można podzielić na dwie części: 1. Odpowiadającą efektom niegenetycznym i 2. odpowiadającą efektom genetycznym. Zatem model można zapisać:

y = X_r α_r + X_a α_a + Z s + e

Wówczas równanie Hendersona (z trzema gwiazdkami - ***) przyjmie postać:

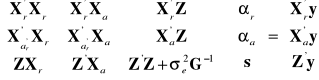
Wygodniej je przedstawić w postaci jak niżej

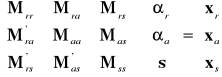
Macierz współczynników powyższego układu równań jest symetryczna i została podzielona na podmacierze oznaczone literą M. Pierwszy wskaźnik przy symbolu M wskazuje jakiego typu efekty wskazują wiersze, drugi zaś jakiego typu efekty wskazują kolumny.

M_ra = X^'_rX_a = [n_ij..]

M_rs = X^'_rZ = [n_ijk.]

M_as = X^'_aZ = [n_.jk.]

Macierze M_rr i M_aa są macierzami diagonalnymi, w których na przekątnej występują liczebności n_i..(macierz M_rr) oraz n_.j. (macierz M_aa ). Wiersze macierzy M_rs odpowiadają grupom niegenetycznym, a kolumny ocenianym osobnikom. Wiersze macierzy M_as odpowiadają grupom genetycznym. Ponieważ oceniany osobnik występuje tylko w jednej grupie genetycznej, elementy niezerowe w tej macierzy mogą wystąpić tylko na przecięciu kolumny danego osobnika z wierszem jego grupy genetycznej.

Macierz M_ss jest sumą macierzy Z^'Z oraz σ²_eG^-1. Z^'Z jest macierzą diagonalną, w której na przekątnej głównej występują liczebności n_.jk. Jeżeli efekty ocenianych osobników, s_jk są nieskorelowane oraz wariancje poszczególnych s_jk są jednakowe i równe σ²_s, to G jest macierzą diagonalną z elementami diagonalnymi σ²_s. Macierz σ²_eG^-1 jest również macierzą diagonalną z elementami σ²_e/σ²_s na przekątnej. W rozpatrywanym przypadku M_ss będzie macierzą diagonalną, w której na przekątnej wystąpią wartości

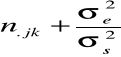
Gdy ocenia się wartość hodowlaną ojców na podstawie ich potomstwa, wtedy

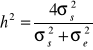
stąd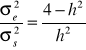

h² oznacza odziedziczalność rozpatrywanej cechy.

Elementami wyrazów wolnych są odpowiednie sumy wydajności.

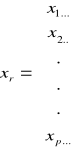
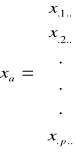
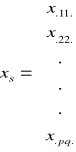
Zadanie

W tabeli podano dane o wydajności córek 4 ojców należących do dwóch grup genetycznych. Odziedziczalność cechy wynosi h² = 0,25, czyli a =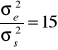
. Dokonaj oceny wartości hodowlanej buhajów metodą BLUP

Grupa genetyczna j	Grupa i Ojciec k	Stado1			Stado2			Łącznie
				Liczba córek	Efektywna liczba córek k-tego ojca	Suma wydajności	Liczba córek	Efektywna liczba córek k-tego ojca	Suma Wydaj- nośći	Liczba córek	Efektywna liczba córek k-tego ojca ć	Suma wydaj-nośći
	1	1	5	3,75	51	-	-	-	5	3,75	51
		2	4	3,20	36	2	1,50	25	6	4,70	61
	2	1	-	-	-	5	1,87	31	5	1,87	31
		2	11	4,95	81	1	0,88	10	12	5,83	91
	Suma	20		168	8	66
	Średnia			8,40		8,25

---