1.Cel ćwiczenia

Wyznaczenie:

-doświadczalne zależność współczynnika oporów liniowych  od liczby Reynoldsa =(Re) na odcinku prostym o długości L.

-objętościowego natężenia przepływu powietrza Q

-bezwzględnej chropowatości przewodu

-doświadczalne zależności współczynnika oporów miejscowych
od liczby Reynoldsa
=
(Re) dla łuku segmentowego oraz łuku kołowego.

2.Wprowadzenie teoretyczne

a)

Gaz rzeczywisty jest lepki i ściśliwy, więc przy przepływie napotyka opory tarcia. Opory te są pokonywane kosztem energii mechanicznej (kinetycznej i potencjalnej), która zamieniana jest na energię cieplną lub energię emitowaną w postaci drgań. Natężenie przepływu mierzone jest na podstawie odczytów ciśnienia dynamicznego w rurce walcowej oraz przy pomocy pierścienia Recknagla

b)opis modelu

Model składa się z następujących elementów:

1) Przewód z blachy stalowej ocynkowanej w części o przekroju prostokątnym a w części okrągłym. Jest w nim wyróżniony odcinek do pomiaru oporów liniowych i kilka elementów do pomiaru oporów miejscowych:

-kratka wyciągowa na zakończeniu łuku kołowego

-łuk kołowy

-trójnik przy przepływie na wprost

-kratka wyciągowa i trójnik przy przepływie pod kątem prostym.

-łuk segmentowy pojedynczy

-łuk kołowy

-łuk kołowy i kratka nawiewna

Wszystkie długości i średnice podane w laboratorium.

2) Rurka walcowa do pomiaru prędkości strugi lub natężenia przepływu w części przewodu o przekroju prostokątnym.

3) Pierścień Recknagla do pomiaru prędkości i natężenia w części przewodu o przekroju kołowym.

4) Przesłona na rolce do zasłaniania kratki wyciągowej.

5) Dziesięciu mikromanometrów kompensacyjnych MK-1 typu Ascania , przeznaczonych do pomiaru ciśnień dynamicznych w rurce walcowej, pierścieniu Recknagla oraz strat ciśnienia na oporach liniowych i miejscowych.

6) Termometru T do pomiaru temperatury powietrza w otoczeniu mikromanometrów.

3.Wyniki pomiarów

lp.	h6[mm]	h7[mm]	h8[mm]	h9[mm]
1	3,36	5	3,74	5,6
2	3,51	4,8	2,15	4,52
3	2,3	3,44	1,94	3,16
4	2,03	3,11	2,84	3,03
5	1,5	2,14	1,38	2,02
6	1,42	2,07	1,33	2,1
7	1,03	1,61	1,08	1,59
8	0,88	1,29	0,77	1,19
9	0,66	1,05	0,68	1,06
10	0,09	0,47	0,33	0,61

Dane

Temperatura	t[C]	24
Gęstość wody	ρH20 [kg/m^3]	997,29
Gęstość powietrza	ρpow.[kg/m^3]	1,16
Kinematyczny wsp. lep. powietrza	v[m^2/s]	0,00000916
Średnica pierścienia Recknagla	DR[m]	0,2
Średnica równoważna przewodu	Dr[m]	0,171575
Przyspieszenie ziemskie	g[m/s^2]	9,81
Wymiary przewodu	a[m]	0,2004
Wymiary przewodu	b[m]	0,15
Dł. prostego odcinka przewodu	L[m]	9,15
Dł. Prze. z zainstalowanym łukiem segm.	Lx[m]	6,47
Ciśnienie atmosferyczne	p [hPa]	990

W celu wyznaczenia liczby Reynoldsa odpowiadającej wyliczonej , musimy odczytać z tablic dynamiczny współczynnik lepkości powietrza w temperaturze 24^oC.

Gęstość powietrza w temperaturze 24^oC (T=297,15K) wyznaczono z równania:

Ciśnienie podczas wykonywania ćwiczenia wynosiło p=990 hPa. Przyjęto, że stała gazowa dla powietrza wynosi R=287,04 J/kg*K.

Zatem:

4. Obliczenia:

• prędkość strugi V i natężenie strumienia powietrza Q

Przykładowy ciąg obliczeniowy dla przykładu 1:

V₀ =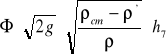
=

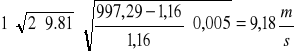
A₀ =
=

Q = V₀ A =

A_p = a*b=0,03006m²

V_p =

gdzie:

V₀ - prędkość w przewodzie kołowym

V_p - prędkość w przewodzie prostokątnym

A₀ - pole przekroju przewodu kołowego

A_p - pole przekroju przewodu prostokątnego

Q - natężenie strumienia powietrza

h₇ - wysokość słupa wody w mikromanometrze do mierzenia obj. natężenia przepływu

H7[mm]	Vo	Q	Vp
0,005	9,18	0,288	9,59
0,0048	8,99	0,282	9,39
0,00344	7,61	0,239	7,95
0,00311	7,24	0,227	7,56
0,00214	6,00	0,189	6,27
0,00207	5,91	0,185	6,17
0,00161	5,21	0,164	5,44
0,00129	4,66	0,146	4,87
0,00105	4,21	0,132	4,39
0,00047	2,81	0,088	2,94

• współczynnik oporów liniowych od liczby Reynoldsa, wyznaczanie bezwzględniej chropowatości przewodu

Przykładowy ciąg obliczeniowy dla 1 przykładu:

λ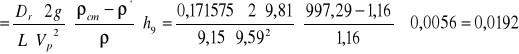

Re
gdzie:

λ - współczynnik oporów liniowych

h₉ - wysokość słupa wody w mikromanometrze do mierzenia oporów liniowych

Re - liczba Reynoldsa

k- chropowatość bezwzględna

W celu wyznaczenia bezwzględniej chropowatości korzystamy z wzoru Colbrooka-White'a:

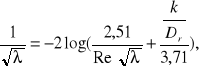
stąd :

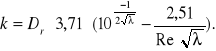
Przykładowy ciąg obliczeniowy dla 1 przykładu:

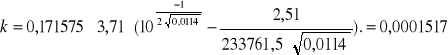
m

Wyniki przedstawiono w tabeli :

H9[mm]	λ	Re	k
0,0056	0,0192	1796292,8	0,0001517
0,0045	0,0162	1758831,1	0,0000678
0,0032	0,0158	1489106,2	0,0000584
0,0030	0,0167	1416055,7	0,0000785
0,0020	0,0162	1174427,1	0,0000651
0,0021	0,0174	1155696,2	0,0000934
0,0016	0,0170	1018960,7	0,0000805
0,0012	0,0159	912194,6	0,0000541
0,0011	0,0174	822286,3	0,0000878
0,0006	0,0223	550688,3	0,0002659

Średnia chropowatość przewodu wynosi k_śr= 0,0001003m

• zależność współczynnika oporów miejscowych ξ od liczby Reynoldsa

Dla przyjętego ε = 5,02*10^-4 zadanej wartości Re odczytaliśmy z nomogramu λ i obliczyliśmy ζ

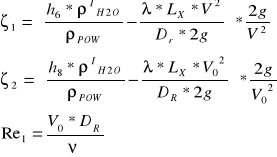
Przykładowy ciąg obliczeniowy dla 1 przykładu:

gdzie:

- współczynnik oporów miejscowych

h₆ - wysokość słupa wody w mikrometrze do mierzenia oporów miejscowych na łuku segmentowym

h₈ - wysokość słupa wody w mikrometrze do mierzenia oporów miejscowych na łuku

*
odczytujemy z wykresu wcześniej wyznaczonej zależności
=
(Re)

h8[mm]	h6[mm]	1(6)	2 (8)	Re2(6)	Re1(8)	λ 8	λ 6
0,00374	0,0034	-0,0248	0,2088	1796292,8	2004366,81	0,017	0,0170
0,00215	0,0035	0,0304	-0,0910	1758831,1	1962882,10	0,017	0,0170
0,00194	0,0023	-0,0272	0,0253	1489106,2	1661572,05	0,017	0,0170
0,00284	0,0020	-0,0419	0,3742	1416055,7	1580786,03	0,017	0,0170
0,00138	0,0015	0,0025	0,1069	1174427,1	1310043,67	0,017	0,0170
0,00133	0,0014	-0,0119	0,1026	1155696,2	1290393,01	0,017	0,0170
0,00108	0,0010	-0,0577	0,1314	1018960,7	1137554,59	0,017	0,0171
0,00077	0,0009	-0,0227	0,0584	912194,6	1017467,25	0,017	0,0172
0,00068	0,0007	-0,0709	0,1074	822286,3	919213,97	0,017	0,0172
0,00033	0,0001	-0,4843	0,1493	550688,3	613537,12	0,0175	0,0175

5.Wnioski.

Na podstawie wykonanych obliczeń zauważono, że wraz ze wzrostem przepływu wzrasta liczba Reynoldsa, a maleje współczynnik oporów liniowych λ.

Podczas analizy wykresu zależności współczynnika oporów liniowych od liczby Reynoldsa stwierdzono, iż większość `punktów' znajduje się w strefie przejściowej. Zatem współczynnik oporów liniowych λ zależy od liczby Reynoldsa oraz współczynnika
. Dlatego też uzasadnione było użycie wzoru Colbrooka-White'a w celu wyliczenia chropowatości bezwzględnej przewodu (dla punktów które zostały umieszczone na wykresie Colbrooka-White'a w strefie przejściowej). Ponieważ nasze ε = 5,02*10^-4 dlatego pozostajemy w strefie przejściowej.

Otrzymane wyniki współczynników oporów liniowych i miejscowych, w niektórych przypadkach odbiegają od wartości tablicowych czego przyczyną mogły być niedokładnie wyniki pomiarów. Sądzimy, iż może to być spowodowane zbyt krótkim czasem stabilizacji wskazań mikromanometrów, w wyniku czego mogliśmy otrzymać błędne wyniki pomiarów. Inną przyczyną może być niedrożność przewodów impulsowych, wywołana przez zanieczyszczenie lub jego załamanie. W niektórych przypadkach wartości oporów miejscowych wyszły ujemne, co oznaczałoby że nie ma oporów miejscowych, co wydaje się nie możliwe.

---