022 023

Ifa rys. 1.9 przedstawiono kod „1 z 10” dla cyfr dziesiętnych.

Zwróćmy uwagę, że np. wprowadzając cyfrę dziesiętną z klawiszy kalkulatora elektronicznego w istocie zadajemy ją w kodzie „1 z 10". Wprowadzając np. cyfrę 7 wciskamy klawisz odpowiadający tej cyfrze co odpowiada podaniu 1 na tej pozycji, zaś wszystkie pozostałe są wyciśnięte co odpowiada podaniu 0 na pozostałych pozycjach.

1.2.7. Kody alfanumeryczne .

Oprócz cyfr często w układach cyfrowych zachodzi potrzeba reprezenta-oji innych symboli w systemie dwójkowym. Kody, które przedstawiają zarówno cyfry, litery jak 1 inne symbole nazywają się kodami alfanumerycznymi. Są one stosowane najczęściej przy komunikacji urządzenia cyfrowego z otoczeniem (np. operatorem) poprzez tzw. urządzenia zewnętrzne, Urządzenie cyfrowe operuje zwykle własnym kodem, a gdy' zachodzi potrzeba np. wyprowadzenia danych, wyrażane są one w kodzie alfanumerycznym i wysyłane do urządzeń wyjściowych jak np. elektryczna maszyna do pisania, różnego typu drukarki, perforatory taśm i kart czy monitory ekranowe. V przypadku wczytywania, urządzenie cyfrowe otrzymuje informacje w kodzie alfanumerycznym z urządzeń wejściowych Jak dalekopisy, czytniki taśm lub kart perforowanych, czytniki taśmy magnetycznej, po czym zamienia Je na swój kod wewnętrzny.

W praktyce korzysta się z kilku standardowych kodów, których typowym przykładem jest przedstawiony na rys. 1.10 7 bitowy kod ASCII (zwany równic! kodem ISO-7). Oprócz reprezentacji cyfr, liter i znaków specjalnych kod ten zawięra także szereg symboli mogących służyć do sterowania urządzeń drukujących (powrót karetki, nowa linia ltp. w przypadku dalekopisu).

			0 0 1
i	0	11
•	0	11
i	t	1 1
i	t	t 1
t	ł	11
l	t	1 1
l	i	i 0
l	i	1 1	u.
i	«	1 0	i
i	i	11	£
l	i	i i
t	0	t 1	i
t	1	0 0	X
i	1	0 1
i	\	t 1
i	\	\ 1

1 0 0	l 0 1	0 i 0
	P	(«)
A	a	I
t	a	1
C	s	*
B	T	•
E	U	*
F	V	*
t	W	1
H	X	(
I	a	)
J	i	*
l	[	+
L	\	)
H	3	—
N	A	•
0	-	/
Rys. 1	.10. Kod ASCII

Ot t i 1 0    111

\	P
4	<V
b	r
c	$
d	t
C	u
f	V
9	w
h	X
i	y
j	i
k	l
l	j
m	}
n	~
0	(»)

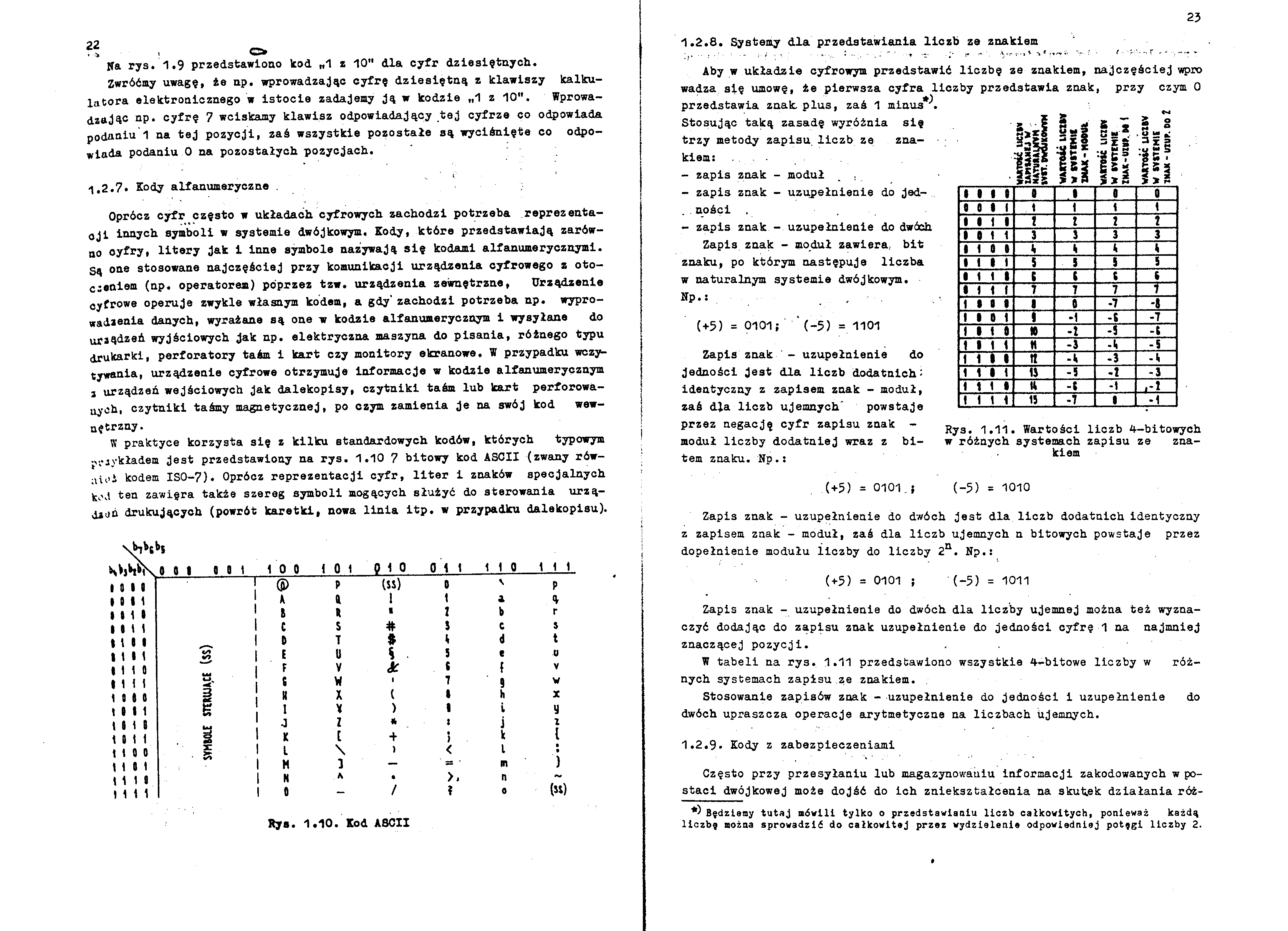
1.2.8. Systemy dla przedstawiania liczb ze znakiem

Aby w układzie cyfrowym przedstawić liczb; ze znakiem, najczęściej wpro wadza się umowę, że pierwsza cyfra liczby przedstawia znak, przy czym O przedstawia znak. plus, zaś 1 minus*\

Stosując taką zasadę wyróżnia się trzy metody zapisu liczb ze znakiem!

1	1	1	t	a	1	i	t
0	0	1		i	1	i	ł
1	1	1	1	i	I	j	7
1	I	1	1	i	J	i	3
1	1	a	ł	k	ł	k	k
•	1	1	1	s		%	i
1	i	1	1	t	(	t	i
1	1	«	1	7	7	7	1
1	1	0	1	1	t	-7	-ł
1	1	t	i	1		-t	-7
1	1	ł	t	»		-J	-t
1	1	t	1	N		-li	-S
i	1	i	l	tt		-3	-i
1	1	I	t	U	-5	-I	-S
I	1	\	i	U	-C	-1	r*
ł	1	1	i	U		1	-1

-    zapis znak - moduł

-    zapis znak - uzupełnienie do Jed-..ności .

-    zapis znak - uzupełnienie do dwóch

Zapis znak - moduł zawiera, bit znaku, po którym następuje liczba w naturalnym systemie dwójkowym. Np.:    .    • .

(+5) = 0101;    ’ (-5) = 1101

Zapis znak ' - uzupełnienie do jedności jest dla liczb dodatnich: identyczny z zapisem znak - moduł, zaś dla liczb ujemnych' powstaje przez negację cyfr zapisu znak -moduł liczby dodatniej wraz z bitem znaku. Np.:

Rys. 1,11. Wartości liczb 4-bitowych w różnych systemach zapisu ze znakiem

(-5) = 1010

(+5) = 0101.1

Zapis znak - uzupełnienie do dwóch jest dla liczb dodatnich identyczny z zapisem znak - moduł, zaś dla liczb ujemnych n bitowych powstaje przez dopełnienie modułu liczby do liczby 2ⁿ. Np.!

(+5) = 0101 ;    (-5) = 1011

Zapis znak - uzupełnienie do dwóch dla liczby ujemnej można też wyznaczyć dodając do zapisu znak uzupełnienie do jedności cyfrę 1 na najmniej znaczącej pozycji.

W tabeli na rys. 1,11 przedstawiono wszystkie 4-bitowe liczby w różnych systemach zapisu ze znakiem.

Stosowanie zapisów znak - uzupełnienie do jedności 1 uzupełnienie do dwóch upraszcza operacje arytmetyczne na liczbach Ujemnych.

1.2.9* Kody z zabezpieczeniami

Często przy przesyłaniu lub magazynowaniu informacji zakodowanych w postaci dwójkowej może dojść do ich zniekształcenia na skutek działania róż-

Będziemy tutaj mówili tylko o przedstawianiu liczb całkowitych, ponieważ każdą liczbę można sprowadzić do całkowitej przez wydzielenie odpowiedniej potęgi liczby 2.