129

Model określonego zjawiska wyraża podstawowe wiadomości o nim za pomocą umownych clcm.-n: , Na przykład wykres:

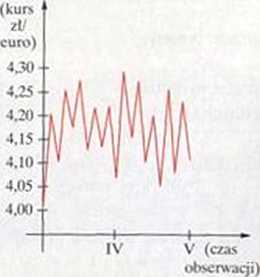
b) jest modelem kursu euro w kwietniu i maju.

a) jest modelem po/iomu

temperatury chorego podczas hospitalizacji.

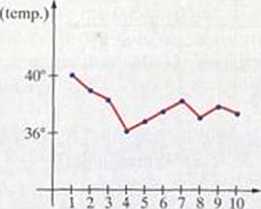
(dni pobytu pacjenta w szpitalu)

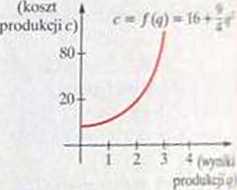
c) przedstawia krzywą callu w -kosztów o równaniu

Q «

c = 16+ j(/\ która jot modelem kosztu produkcji w zależności od wiclkn-o wyników produkcji.

4. FUNKCJE

CD

d) jest modelem przebytej ze stalą prędkością drogi w zależności od czasu.

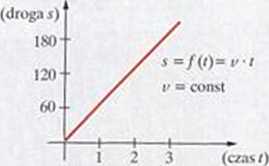
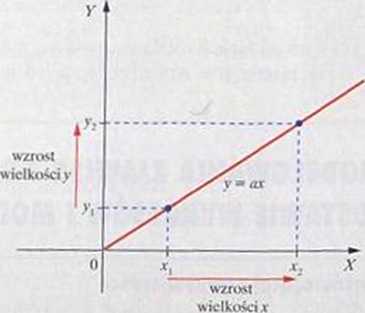
Dwie wielkości są wprost proporcjonalne, jeśli zwiększenie (lub zmniejszenie) jednej z nich (np. s) powoduje równocześnie zwiększenie (lub zmniejszenie) drugiej (np. t). przy czym stosunek tych zmian jest stały (np. v = j). Funkcja y =qx (a / 0) jest modelem wielkości wprost proporcjonalnych x i y o współczynniku proporcjonalności u (por. 4.5.).

.    p

e) przedstawia krzywą popytu o równaniu P~ która jest modelem ustalanej ceny pewnego dnFr w zależności od planowanej na sprzedaż jego iW

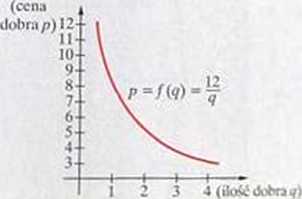
Dwie wielkości są odwrotnie proporcjonalne

zwiększenie (lub zmniejszenie) jednej / nich (np powoduje równoczesne zmniejszenie (lub zwichnie) drugiej (np. p), przy czym stosunek tychzrr .a jest stały (np. 12). Funkcja y j (a ?- 0. i ^{1 1} ,v modelem wielkości odwrotnie proporcjonalny^

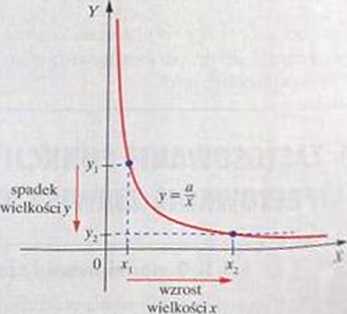
Dla wielkości odwrotnie proporcjonalnych

jest ich iloczyn: x y - o.

Dla wielkości wprost proporcjonalnych stały jest ich iloraz (stosunek): ^ = a. zwany współczynni-kicm proporcjonalności.

4.4.2. Odczytywanie własności funkcji z jej wykresu (por. 4.1.6.)

Największą rolę w analizie określonego fragmentu rzeczywistości odgrywają wykresy prezentujące własno-<1 i dynamikę wybranych zjawisk. Analizując wykres (model), można wyciągać różne w nioski o przebiegu •• redstaw ianego zj aw i ska.

Oto podstawowe własności, które odczytujemy, Wizując wykres określonej zależności - funkcji.

Dany jest wykres funkcji y =/( x).

Na podstawie wykresu będą odczytywane niżej wymienione własności funkcji.

(IWłWlC Kr»tkl

>v<w/aj4 pnwoLfim irol »>krnu u ot Oł)

(pionowe tu/i&i

anx/a’)4 pfMofc^lm troi ») krcvu na vi OX)

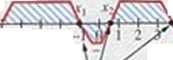
i) Dziedzina i zbiór wartości (por. z 4.1.6a.) Na rysunku D. = (-5:8). K_w = (-4:3).

b) Miejsca zerowe (por. z 4.1.6b.)

Na rysunku punkty przecięcia wykresu z osiąOA' to: (-1:0),|    0 ^. (3.7^; 0).

Zatem są trzy miejsca zerowe: x, = -1. x_: = y. .v, = 3.7.

c) Znaki funkcji (fw>r. 4.1.6c.)

Znaki funkcji, której wykres jest przedstawiony tu rysunku powyżej, można zilustrować następująco:

A więc:

f{x)> 0dla.ee (-5: -l) U |y:3.7 j -funkcja jest znaku dodatniego,

/(i) < Odla.r <5 (-1:4-) U (3.7:8)

- funkcja jest znaku ujemnego.

(znak

dodatni)

+ + /(¹) >«

. (w>krc» i»m1 0114 OX)

(rtr.)-O) (/(»;)“0) (flr,)«0)

-5 -4

(znak

ujemny)    A O <⁰

(miejsca zerowe) (wykres pod om.) OX)

•V

4. FUNKCJE

górna

Pła

szczyzna

dolna

pólpla-

nczyzna

CzZ.

CZ>

d) Monotoniczność (por. 4.1.6d.)

Munotoniczność funkcji, której wykres jest przedstawiony na rysunku, można zilustrować następująco:

// /conw    f\

/S/OOIIM /\ f/

*

-5 -4 -3 -2 -1012 3 4 5 6 7

Funkcja jest monotoniczna w niektórych przedziałach: funkcja rośnie ( / /) w trzech następujących przedziałach: (-5; — 4 ). (0; 3). (7:8)

•funkcja maleje (/ \)w trzech następujących przedziałach: (-3:0). (3:4).(5:7).

1

I Wartość największa i najmniejsza funkcji (por. 4.1.6e.)

n ; pierwszy m rysunku mamy: dla x = 3, /(3) = 3 i to jest największa wartość funkcji (większej nie ma), dlt.t 7,/(7)    -4. i to jest najmniejsza wartość funkcji (mniejszej nic ma).

Zatem wartości największej na wykresie odpowiada punkt (3:3) (najwyżej położony), a wartości najmnięj-',] punkt (7: 4) (najniżej położony).