13598 Untitled Scanned 86 (2)

ZADANIA OPTYMALIZACYJNE

613. n Drut o długości 28 cm należy podzielić na dwie części i z jednej zrobić kwadratowa ramkę, a z drugiej ramkę prostokątną, której jeden bok jest trzy razy dłuższy od drugiego. Jak należy podzielić drut. jeżeli chcemy, aby suma pól otrzymanego kwadratu i prostokąta była najmniejsza?

614. Drut o długości 72 cm rozcięto na dw a kawałki i z każdego kawałka zbudowano brzeg trójkąta rów nora- I micnnego. przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi 5:8. I a w drugim 13: 10. Jaki obwody mają te trójkąty, jeżeli suma ich pól jest najmniejsza z możliwych?

615.    Na bokach prostokąta o obwodzie 16 cm opisano, jako na średnicach, półokręgi leżące na zewnątrz pro- I stokąta. Zbadaj, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech pólokręgów jest najmniejsze. Oblicz to pole.

616.    w Suma długości dwóch boków trójkąta jest równa I2 cm. a kąt między tymi bokami ma miarę 30°. Oblicz, I

jakie powinny być długości boków tego trójkąta, aby jego pole było największe.

617. Obwód trójkąta równobocznego ABC jest równy 12 cm. Punkty M, N. P należą odpowiednio do boków I AB. BC i A(' tego trójkąta, przy czym | AM I -1 BN | = | CP | = ,v. Zbadaj, dla jakiej wartości x pole trójkąta I MNP będzie najmniejsze. Znajdź wartość tego pola.

618. R Zbiór 7" jest zbiorem wszystkich trapezów o obwodzie 60 cm i kącie ostrym, którego sinus jest równy 0,75. Znajdź długość ramienia tego trapezu należącego do zbioru 7'. który ma największe pole.

619. fi W trójkąt prostokątny «> przy prostokątnych długości (> i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych. a jeden z wierzchołków leży na przeciw pr ostokątnej. Zbadaj, jakie I powinny być wymiary prostokąta, aby jego pole było możliwie największe.

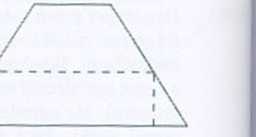
620. Z kawałka blachy w kształcie trapezu równoramiennego o polu 1.2 nr i podstawach długości 60 cm i I4l> cm należy wyciąć (w sposób pokazany na rysunku) prostokątny fragment o maksymalnym polu. Jakie wymiary będzie miał wycięty prostokąt?

621.    R W trójkąt prostokątny o kącie ostrym 30° i przeciwprostokątnej długości 40 cm wpisujemy prostokąty

w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta Zbadaj, który / tych prostokątów ma największe pole.

622.    W Boki trójkąta prostokątnego ABC mają długości: !,4C|= 3. IRC'\~ 4. U/?|= 5. Prosta /. równoległa J

prostej AB. przecina boki AC i BC odpowiednio w punktach M i jV. Niech S oznacza środek odcinka AB oraz MC i =x.

a)    Pole P(x) trójkąta MNS jest funkcją zmiennej x. Znajdź wzór tej funkcji.

b)    Zbadaj, jaką największą wartość może przyjmować pole trójkąta MNS.

Suma długości wysokości trapezu równoramiennego i obu jego podstaw jest równa s. Wyznacz tangeiu kąta. jaki tworzy z podstawami przekątna tego trapezu, wiedząc, że jego pole jest największe z możliwych.

623.