Untitled Scanned 84 (2)

5. ZADANIA OPTYMALIZACYJNE

ZADANIA WPROWADZAJĄCE

Zdający potrafi

wykorzystywać własności funkcji kwadratowej i jej wykresu do io/H'i;\/ywania zadań optymalizacyjnych

5.1    R /.najdź, takie dwie liczby, których różnica jest równa 10. a ich iloczyn jest najmniejszy z możliwych.

5.2    R Jakie największe pole może mieć trójkąt, w którym suma długości jednego z boków i wysokości poprowadzonej

z wierzchołka nienależąccgo do tego boku wynosi 12 cm?

5.3    R Na dwusiecznej kąta prostego trójkąta prostokątnego o wierzchołkach A = ((). 0). li ó3- <J). C = (0, 3) znajdź taki

punkt aby suma kwadratów odległości punktu P od wierzchołków trójkąta była najmniejsza.

5.4    R Nauczyciel matematyki polecił uczniom wykonać następujące zadanie praktyczne: „z kowalki (Innu o długości

80ciii nylonu/- szkielet prostopadłościanu o podstawie kwadratowej i o największym polu powierzchni horzjicf. Oblicz pole powierzchni tego prostopadłościanu.

ZADANIA MATURALNE

PLANIMETRIA

609. R Ratownicy mający do dyspozycji linę długości 80 metrów mają wytyczyć przy brzegu plaży kąpielisko w kształcie prostokąta (wzdłuż brzegu nic będzie liny). Jakie wymiary powinno mieć to kąpielisko, jeżeli wczasowicze chcą. aby miało ono jak największą powierzchnię? Należy przyjąć, że brzeg plaży tworzy linię prostą.

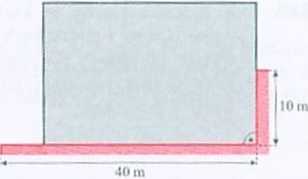
610. Deweloper przed rozpoczęciem inwestycji zamierza ogrodzie fragment działki, na którym będą składowane materiały budowlane. Skład materiałów ma mieć kształt prostokąta, a część ogrodzenia stanowić będzie istniejący mur (tak jak na rysunku). Na ogrodzenie składu zakupiono 50 metrów drucianej siatki. Jaką maksymalną powierzchnię może mieć skład materiałów budowlanych?

611. W punkcie skupu trzody chlewnej należy zbudować ogrodzenie ograniczające trzy jednakowe prostokątne boksy (patrz rysunek). Właściciel skupu zakupił materiały pozwalające zbudować ogrodzenie o łącznej długości 48 m i chce. aby powierzchnia boksów była możliwie największa. Jakie powinny być wymiary każdego boksu?

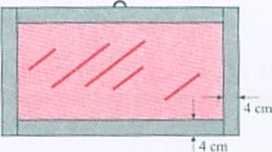
612. Drewnianą listwę o długości I m i szerokości 4 cm należy pociąć na takie cztery części, aby po ich sklejeniu (w sposób pokazany na rysunku) otrzymać ramę, w- którą można oprawić obraz. Oblicz maksymalne pole powierzchni obrazu, który może być oprawiony w tak zbudowaną ramę.