17508 PC043399

110

Wielomiany są równe, jeśli współczynniki przy odpowiednich je« są równe, czyli:

f >4+5=3

3A-3B+C=-4.

4A-3C=7

Rozwiązaniem ukiadu są liczby A = 1,5=2 oraz C = -1. Funkcja/

x-3 x“+3+4

jako suma ułamków prostych ma postać f(x)=

b) Mianownik funkcji jest zapisany w postaci iloczynowej. Poniewa z pierwiastków mianownika jest podwójny, rozkład na ułamki prostepn

, 5x²+10x+3 AB C _Vł, .

postać--=—-+—-+-7. Należy wyznaczyć wspołc

(x-l)(x+2)‘    (x+2)²    :

ki A. B oraz C. W tym celu sprowadzamy prawą stronę równania do wspói mianownika i grupujemy odpowiednie wyrazy licznika. Otrzymujemy: *

5x² + 10x+3 (A+B)x² +(4A+B+C)x+4A-2B-C

(x-l)(x+2)

(x-l)(x+2)

Porównując odpowiednie współczynniki liczników, uzyskujemy zależni

Stąd >4=2,5=3, C=-1. Funkcję g możemy więc zapisać w postaci:

A+B=5

4A+B+C=10.

4A-2B-C=3

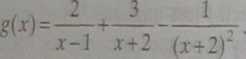
c) Zauważmy, że dla trójmianu r + 2x + 3 mamy A = 4 -12 = -8 < 0, zaic nie da się go rozłożyć na czynniki liniowe. Funkcja h w rozkładzie na uw proste przyjmuje postać:

4x⁴ + \\x^} +25x² +2\x + 28 _ A Bx+C Dx+E 1

i{^+2i+3)²    | *1111

Zależność ta generuje układ równań

>4+5=4 4>4+25+C=ll 10>4 + 35+2C+Z)=25, 12>4 + 3C+£=2I 9/4=18

którego rozwiązaniem są liczby A =2,fl = 2.C = -l.D- 1 oraz £ = 0. Funkcję h możemy zapisać w postaci:

., _x 2    2x— 1    x

«(*)=—+—5-+—5-r-

* x² +2x+3 (x²+2z + 3 :)■

d) W tym przykładzie stopień licznika jest większy od stopnia mianownika, zatem najpierw wykonujemy dzielenie wielomianów:

2 a-⁵ + 3x⁴ + 3x³ + 7x²+4x+8 _    _ x³+4x²+2x+5

- ---;—= 2x+3+--5-.

X + X +1    X +x +1

Teraz należy rozłożyć mianownik funkcji k na czynniki. W tym celu należałoby rozwiązać równanie x⁴ + Z² + 1 = 0. Jest to tzw. równanie dwu kwadratowe. Po podstawieniu pomocniczej niewiadomej z² = t otrzymujemy równanie t² + t + 1 = 0, które nie posiada rozwiązania. Zatem ten sposób rozkładu na czynniki zawodzi. Aby zapisać wyrażenie x⁴ + r+lw postaci iloczynowej, należy wykonać następujące przekształcenia:

x⁴+z² +1 =x^Ą + 2x? +1 —X² - (z² + l)²-x² = (z² +1 -zK*² +1 +z) =

= (x²~x+ l)(;r+z+l).

Żaden z czynników powyższego iloczynu nie jest rozkładałny. A zatem rozkład na czynniki wielomianu z⁴ + z² + 1 ma postać (z² -z + l)Qr -rz- 1). Rozważane wyrażenie przedstawimy teraz w postaci ułamków prostych:

x³-h4x²-t-2z+5 _ Ax+B , Cx + D x⁴+z²+l z^:-z+l z*+z+l Otrzymujemy układ równań:

A+C = 1 A+B—C + D=4 A+B+C-D—l'

B+D=5

którego rozwiązaniem są liczby A = 0. B = 3, C = 1 oraz D = 2. Ostatecznie:

3    x+2

fc(z)=2z+3-i—5-+—--

z‘-z+l x“+z+l

Równania i nierówności wymierne

Rozwiązaniami równania wymiernego, czyli rówmania postaci    =0. gdzie

W i G są wielomianami, są wszystkie liczby rzeczywiste spełniające warunki: JP(*) = 0aG(x)*0.