122536

położenia równowagi. Obliczyć prędkość ciała w chwili zderzenia, jeśli współczynnik tarcia kinetycznego między ciałem a poziomą powierzchnią, równy jest/.

3. Zasada zachowania pędu i energii mechanicznej

1.    Kula drewniana o masie M ułożona została na metalowym pierścieniu zamocowanym w statywie. Z dołu w kulę trafia pocisk o masie m lecący pionowo do góry i przebija ją. W wyniku tego zderzenia kula podnosi się na wysokość h. Na jaką wysokość H podniesie się pocisk, jeśli jego szybkość przed zderzeniem wynosiła v.

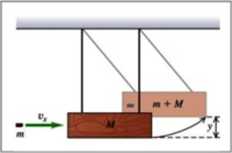
2.    Rysunek przedstawia wahadło balistyczne służące do pomiaru prędkości pocisków. Kula o masie m_k wystrzelona poziomo uderza z szybkością v₀ w drewniany blok o masie M. Zderzenie jest całkowicie niesprężyste, a blok wychyla się na wysokość h. Znając wartości: m^ M, h oblicz energię kinetyczną kuli i porównaj ją z energią kinetyczną układu po zderzeniu. Czy w czasie zderzenia energia kinetyczna, ew. mechaniczna jest zachowana?

3.    Doskonały karateka łamie drewnianą deskę o masie M = 0,14kg uderzając w nią z góry pięścią o masie m, = 0,70kg. Stała sprężystości deski wynosi k = 4,1 • 10⁴N/m. Deska pęka przy jej wygięciu o d = 16mm. a.Ile wynosi energia zgromadzona w desce tuż przed jej złamaniem? b. Ile wynosi najmniejsza prędkość pięści potrzebna do złamania deski? Załóż, że zderzenie jest niesprężyste, biorą w nim udział jedynie pięść i deska, zginanie deski zaczyna się tuż po zderzeniu, podczas zginania przedmiotu zachowywana jest energia mechaniczna, a gdy przedmiot zaczyna pękać, prędkości pięści i deski są praktycznie równe zeru.

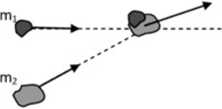
4.    W przestrzeni kosmicznej doszło do niesprężystego zderzenia meteorytu o masie m, =20,0kg z satelitą o masie m₂=500kg . Znajdź wektor prędkości satelity v₂ Jeśli wartość prędkości v_x meteorytu wynosiła lOOOm/s, a po zderzeniu (meteoryt ugrzązł w satelicie) wrak satelity poruszał się z szybkością 66,6m/s pod kątem 30° do kierunku początkowego ruchu meteorytu.

Na następne zajęcia proszę zrobić powyższe zadania oraz nauczyć się materiału z unikładu 5.

Literatura

D.Halliday,R.Resnick,J.Walker: Podstawy fizyki, t.l.

(podręcznik polecany - z niego są zaczerpnięte niektóre tematy zadań) B.Oleś: Wykłady z fizyki, Wydawnictwo PK

A.Januszajtis: Fizyka dla politechnik, t.l

Pytania i zagadnienia, które mogą pojawić się na egzaminie pisemnym

1.    Zasada zachowania energii mechanicznej, a. Wyprowadź wzór na energię kinetyczną ciała.(2p) b. Zdefiniuj energię potencjalną. Podaj wyrażenie na energię potencjalną. (2p) c. Wyprowadź i sformułuj zasadę zachowania energii mechanicznej.(3p) d. Oblicz energię potencjalną meteorytu o masie m znajdującego się w odległości 3R od środka Ziemi. Jeśli meteoryt w odległości 3R od środka Ziemi posiada prędkość v₀, to ile wyniesie wartość jego prędkości w momencie uderzenia o Ziemię? (3p)

2.    Zasada zachowania energii mechanicznej, a. Zdefiniuj energię mechaniczną (podaj wyrażenie na energię kinetyczną i energię potencjalną). (2p) b. Wyprowadź i sformułuj zasadę zachowania energii mechanicznej.(3p) c. Znajdź

2