20122 skanuj0070 (10)

120 B. Cieślar

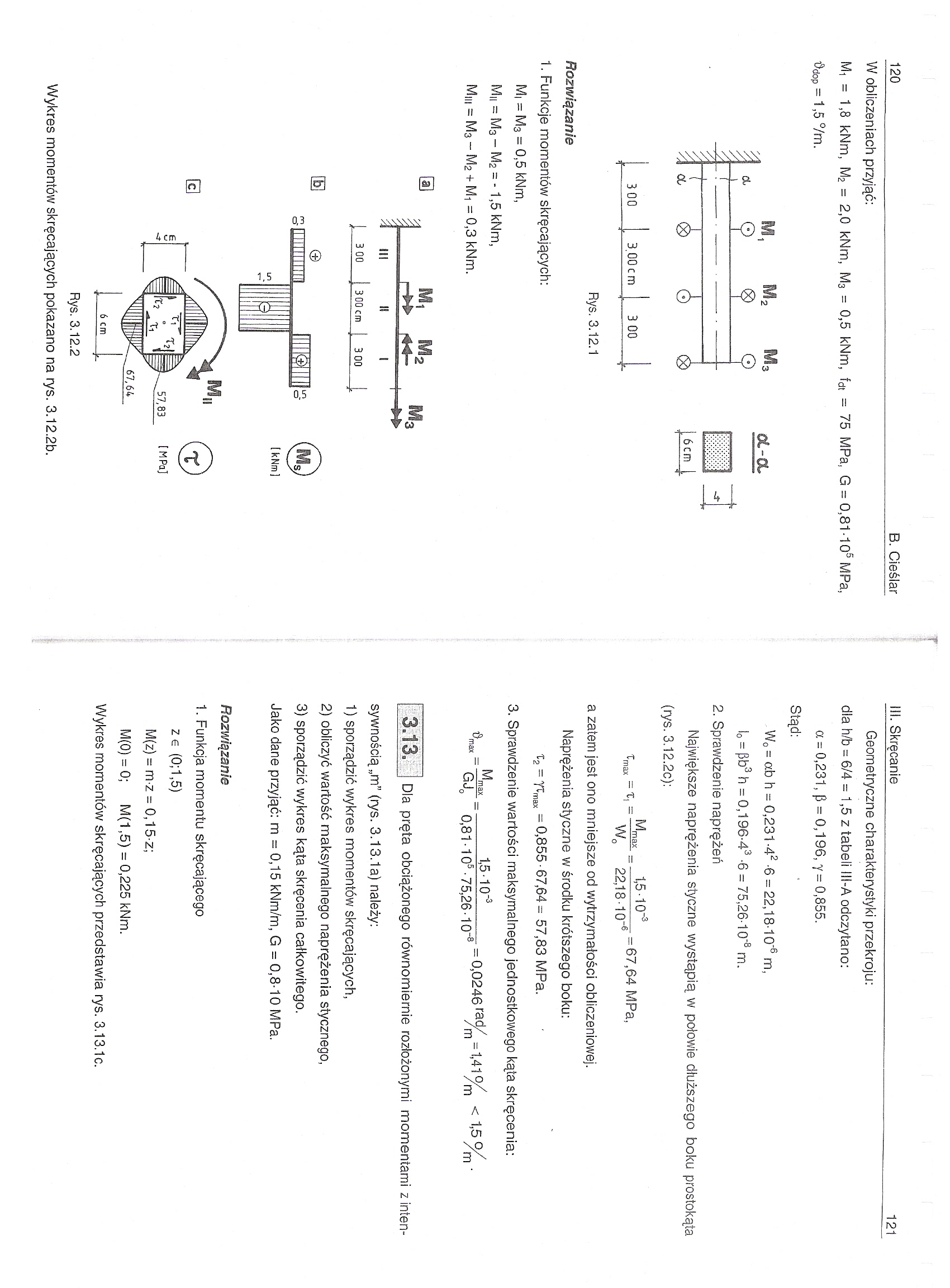
W obliczeniach przyjąć:

Mi = 1,8 kNm, M₂ = 2,0 kNm, M₃ = 0,5 kNm, f_dt = 75 MPa, G = 0,81-10⁵ MPa, •Odop = 1,5 °/m.

M,

;V ^ w	©
1 5	©

3 00

3 00 cm

OC-OL

3 00

Rys. 3.12.1

Rozwiązanie

1. Funkcje momentów skręcających:

Mi = M₃ = 0,5 kNm,

Mn = M₃ - M₂ = -1,5 kNm,

Mm = M₃ - M₂ + Mi = 0,3 kNm.

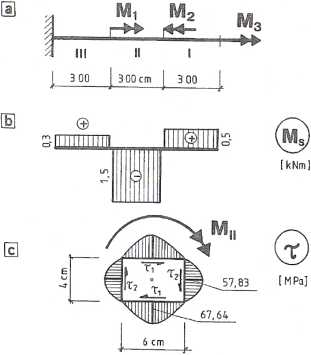
Rys. 3.12.2

Wykres momentów skręcających pokazano na rys. 3.12.2b.

III. Skręcanie__

121

Geometryczne charakterystyki przekroju: dla h/b = 6/4 = 1,5 z tabeli lll-A odczytano: a = 0,231, p = 0,196, y = 0,855.

Stąd:

. W₀ = ab h = 0,231 -4² -6 = 22,18-1 O*⁶ m, l₀= pb³ h = 0,196-4³ -6 = 75.26-10'⁸ m.

2. Sprawdzenie naprężeń

Największe naprężenia styczne wystąpią w połowie dłuższego boku prostokąta (rys. 3.12.2c):

^max

^max

W₀

1,5 10^-3 22,18-10"⁶

= 67,64 MPa,

a zatem jest ono mniejsze od wytrzymałości obliczeniowej. Naprężenia styczne w środku krótszego boku: t₂ = yz^ = 0,855 • 67,64 = 57,83 MPa.

3. Sprawdzenie wartości maksymalnego jednostkowego kąta skręcenia:

1,5-10“

0,81-10^s -75,26-10“

0,0246^ = 1,41?/ <1,5?/

3.13.

Dla pręta obciążonego równomiernie rozłożonymi momentami z inten

sywnością „m” (rys. 3.13.1 a) należy:

1)    sporządzić wykres momentów skręcających,

2)    obliczyć wartość maksymalnego naprężenia stycznego,

3)    sporządzić wykres kąta skręcenia całkowitego.

Jako dane przyjąć: m = 0,15 kNm/m, G = 0,8-10 MPa.

Rozwiązanie

1. Funkcja momentu skręcającego z € (0; 1,5)

M(z) = m-z = 0,15-z;

M(0) = 0;    M(1,5) = 0,225 kNm.

Wykres momentów skręcających przedstawia rys. 3.13.1c.