28358 Untitled Scanned 05 (17)

Momenty węzłowe oznaczymy: M₁₂ — przy węźle 1 dla pręta 1 - 2; M₂₁ — przy węźle 2 dla tegoż pręta; M₂₃ — przy węźle 2 dla pręta 2-3 itd.

Analogiczne oznaczenia przyjmiemy dla sił poprzecznych T (rys. 13.4b). Sporządzanie wykresu T rozpoczniemy np. od rygla. Wyodrębnione przęsło 1 — 2 (rys. 13.4a) rozpatrujemy niezależnie od pozostałych elementów jak jednoprzęsłową belkę.

<D	inmflmi	® ł i
	j	J
	j j	j	-C
@r>	T, 99	© ^ 7*	r,@—
	<«	^2

Rys. 13.2

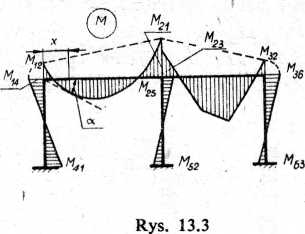
Na belkę tę działa rozłożone równomiernie obciążenie q i momenty podporowe (węzłowe) M₁₂ • M_2x zastępujące oddziaływanie (zginające) na wyodrębniony pręt pozostałych części ramy (rys. 13.4a). Momenty pokazane są jako powodujące rozciąganie dolnych włókien (oznaczane znakiem plus), mimo że z ogólnego wykresu momentów (rys. 13.3) widać, że są one skierowane przeciwnie (ujemne). Należy tu wyjaśnić, że przy rozwiązaniu w formie ogólnej dla uniknięcia omyłek przyjmujemy dowolne zwroty wszystkich wielkości traktując je jako dodatnie, znaki rzeczywiste zaś uwzględniamy w chwili podstawiania wartości liczbowych.

<9	Q
jTrrnTrmrnTTT	Tirf
A © b)	A ©
	-T.

Rys. 13,4

Siła poprzeczna przy lewej podporze równa jest lewej reakcji podporowej; wyznaczamy ją z warunku równowagi sumy momentów względem prawej podpory:

(13.5)

n A/₂j Af12 _n nr O . ^z 1    1 z

i

12 “^12 “ ¹12 "r "

12

gdzie T°₂ — siła poprzeczna dla belki swobodnie podpartej wywołana danym obciążeniem (a więc bez uwzględnienia momentów M,₂ i M₂₁); w danym przypadku Ti2—ql_l2/2 .

Siła poprzeczna przy prawej podporze równa się prawej reakcji podporowej z odwrotnym znakiem'.

r₂i = -^₂₁ = r₂⁰1 +

(13.6)

M₂₁ — M12

gdzie T°i = —<?/₁₂/2 .

443