46202 Untitled Scanned 08 (17)

(por. twierdzenia redukcyjne w [16]). Tak więc:

- fMjM    fiy.-N _ f'/] T _P , f Mi<xAt

*•■=?-) ~źr^js+^yn^ds+1,,\    ^N'“"^,s+£j ~r~^ds+

— R,R _ Mi M _

+I-^-+E —(13.9)

łC    K

W zależności od typu podpór, obciążeń i od tego, czy uwzględniamy wpływ sil poprzecznych i podłużnych na przemieszczenia rozpatrywanego układu ramowego, będziemy uwzględniać wszystkie lub tylko niektóre wyrazy wzoru (13.9). W przypadku szczególnym, lecz często spotykanym, gdy rama ma podpory niepodatne, pręty prostoliniowe, jest obciążona jedynie siłami zewnętrznymi oraz pomijamy wpływ (zwykle bardzo nieznaczny) sił poprzecznych i podłużnych na przemieszczenia, wzór (13.9) przybiera postać:

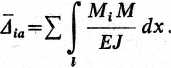
(13.10)

13.4. Kontrola wyników

Zgodnie z ogólnymi zasadami omówionymi w p. 9.8, obowiązuje przeprowadzanie kontroli w trakcie obliczeń oraz sprawdzenie wyników końcowych.

Często, choć niesłusznie, uciekamy się do kontrolowania obliczeń początkowych dopiero wówczas, gdy uzyskamy negatywne efekty sprawdzenia wyników końcowych.

13.4.1. Kontrola wykresów dla układu podstawowego

W równaniach kanonicznych metody sił, jak wiemy, współczynniki przy niewiadomych przedstawiają przemieszczenia układu zastępczego (podstawowego) od jednostkowych wartości niewiadomych, a wyrazy wolne przemieszczenia od obciążeń zewnętrznych. Przemieszczenia te dla ram wyznaczamy wg wzorów (13.1)-r-(13.3).

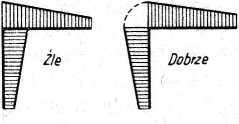
Rys. 13.8

Najpierw sprawdzamy prawidłowość wykonania wykresów momentów zginających od obciążeń jednostkowych i zewnętrznych. Kontrolujemy więc, czy wykresy momentów były zawsze konsekwentnie odkładane, po stronie włókien rozciąganych i czy spełniają one warunki równowagi. Na rys. 13.8 pokazano wykres momentów nie spełniający warunku równowagi węzła i wykres spełniający ten warunek.

446