29843 Skrypt PKM 1 00035

70

Siłę określimy z warunku równowagi Równanie powyższe można przedstawić w postaci

dN, „    dtf,    dN*

-r-* = 2rflt, -r- =    .

dx    dx    dx

(2.1)

Kąt odkształcenia postaciowego w zakresie odkształceń sprężystych

T

y ~ TT*

Go

gdzie

^G° 2(1 +

- moduł odkształcenia postaciowego spoiwa.

W oparciu o równanie (11) można zapisać

1 dN_z ^y 2naG₀ dx

(2.2)

Zmiana kąta y na odcinku dx (rys. 120 b) związana jest ze zmianą deformacji rur> na tym odcinku, stąd

<h N_t-N_x

dx

do c

c = EF = 2 nagE

(2.3)

gdzie:

c

£

F

-    sztywność rury na rozciąganie,

-    moduł sprężystości rury na rozciąganie,

-    przekrój rury.

We wzorze (13) — oznacza przemieszczenie na odcinku AB, a ~ przemiesz-

c    c

czenic na odcinku CD zgodnie z rys. 2.20 b. Po wykorzystaniu (2.1) i podstawieniu

do (13)

(14)

djV ₌ G₀(2N — Q) ** gEgo

gdzie:

Wzór (2.4) można zapisać

gdzie:

N" - u)²N

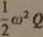
(2.5)

2 G

Rozwiązując powyższe równanie znajdziemy

N

= ₂Q + C_t sin/: (to jc) + C₂co$h(iox).

(2.6)

Można wykazać, że dla warunków brzegowych: jc = 0, N = 0 oraz x — l, N = Q otrzymamy

(2.6)

(17)

_ 1    1 +cos h(a>l)    l

¹    2* sinh(o>/) *    2^Q

Po wykorzystaniu (2.6) otrzymamy

1 dN

2 xadx'

dN

dx

Q • co cos h (tux) + cos h w(l - x) 2    sin h (co l)

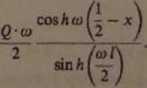
Na rys. 121 pokazano wartość t(x) wg (17) oraz naprężenia tnące nominalne obliczone wg wzoru

(2-8)

Q

^T" 2 nal