51844 skanuj0085 (31)

150 B. Cieślar

Z tablic przyjęto 2 dwuteowniki 340p o W_x = 2-890 = 1780 cm³. Sprawdzenie naprężeń:

150 B. Cieślar

maxO=^n&=191.0 MPa < f_d.= 215 MPa. 1780-10^-6

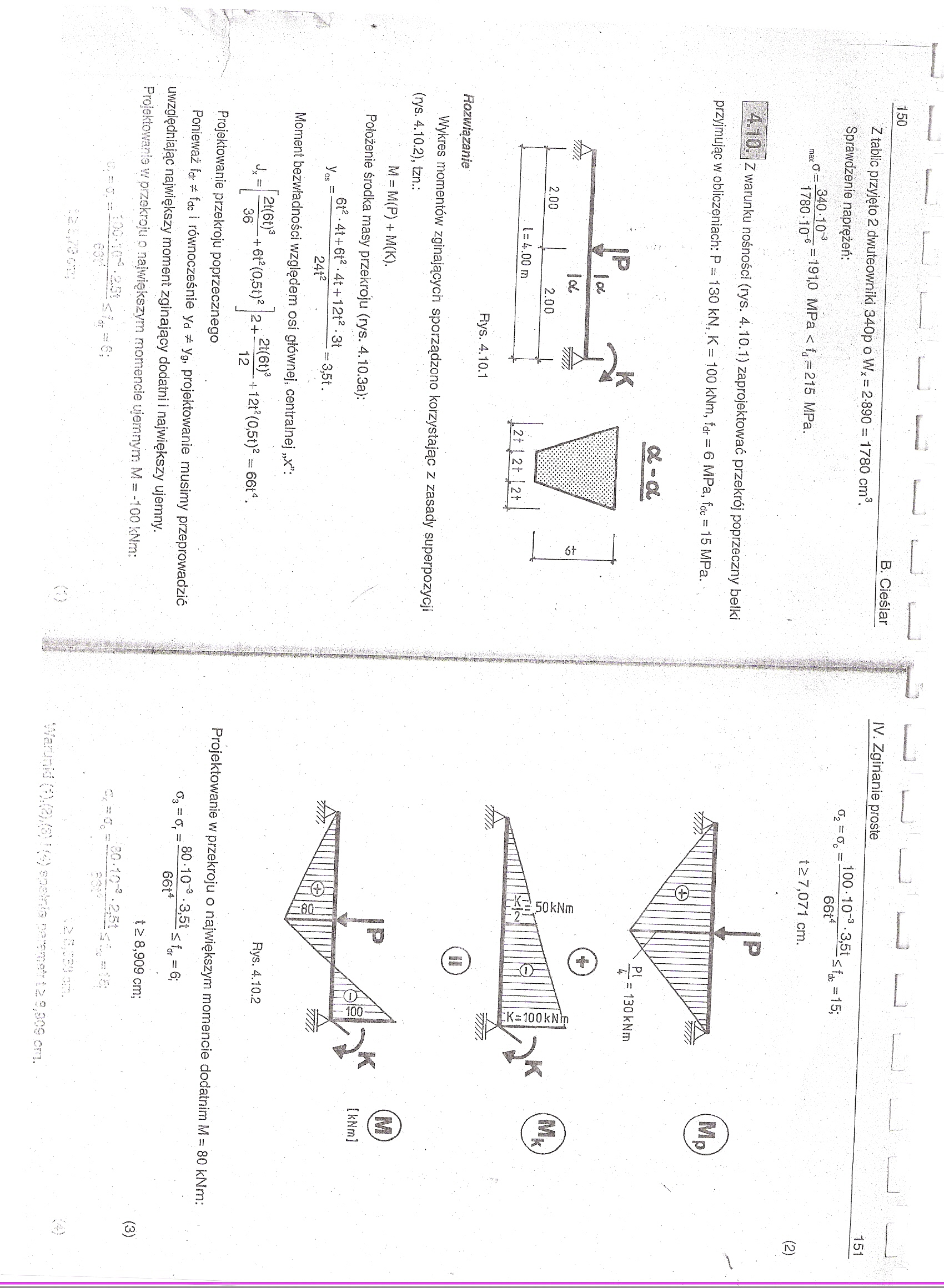
przyjmując w obliczeniach: P = 130 kN, K = 100 kNm, f_dr = 6 MPa, f_dc = 15 MPa.

ct-oc

K

Rys. 4.10.1

Rozwiązanie

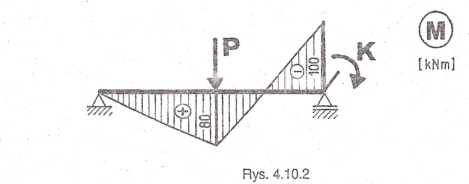
Wykres momentów zginających sporządzono korzystając z zasady superpozycji (rys. 4.10.2), tzn.:

: M = M(P) + M(K).

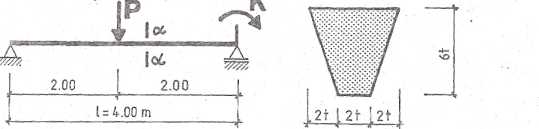
Położenie środka masy przekroju (rys. 4.10.3a):

6t² -4t+6t² -4t+12t^z -3t *»=-24?-:—

Moment bezwładności względem osi głównej, centralnej „x”:

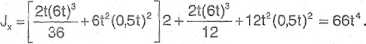
Projektowanie przekroju poprzecznego

Ponieważ f_dr ^ f* i równocześnie y_d & y_g, projektowanie musimy przeprowadzić uwzględniając największy moment zginający dodatni i największy ujemny. Projektowanie w przekroju p największym momencie ujemnym M = -100 kNm:

I ■ _    100-10^-3 -3,5t,,,

15;

(2)

= O? -——“2—— S Tj.

^{2 c} 66t⁴    *

7,071 cm.

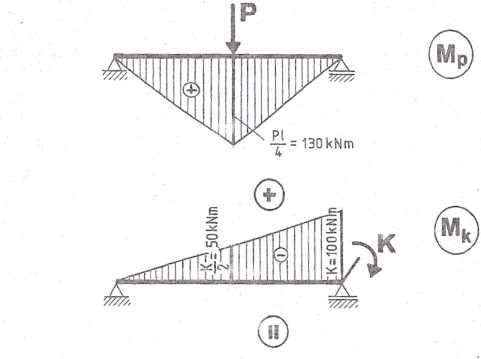
Projektowanie w przekroju o największym momencie dodatnim M = 80 kNm:

6;

_    _    80-10^-3-3,51^,

°³⁼°' ⁼    66t⁴    ~^S<*

t > 8,909 cm;

80 -10"⁸ „

WarUśikł (15,(2),(3)! (4) sps-hiła parwTre-r t > 9,809 cm.

(3)