58675 skanuj0050 (55)

Każda płaszczyzna przechodząca przez trzy węzły jest płaszczyzną sieciową. Zawiera ona nieskończoną liczbę węzłów. Płaska komórka sieciowa to dowolny równoległobok, zbudowany na czterech węzłach płaszczyzny sieciowej. Nazywa się ją komórką prostą, gdy zawiera węzły tylko w wierzchołkach, wielokrotną zaś — gdy węzły znajdują się w jej

o

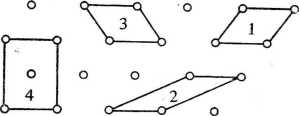
Rys. 1.28. Komórki płaskie; 1, 2,3 — komórki proste, 4 — komórka wielokrotna (podwójna)

o

wnętrzu lub na brzegach (rys. 1.28). Płaska komórka sieciowa jest najmniejszą jednostką, z której wychodząc można utworzyć całą płaszczyznę sieciową przez połączenie identycznych równoległoboków o tej samej orientacji bez pozostawienia między nimi pustych miejsc (rys. 1.29).

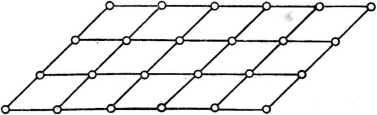
Rys. 1.29. Podział przestrzeni na identyczne równoległoboki o jednakowej orientacji

Komórka sieciowa jest równoległościanem zbudowanym na ośmiu węzłach, tj. na trzech wektorach wychodzących z tego samego węzła i niekoplanarnych. Komórka jest prosta, gdy węzły znajdują się tylko w ośmiu narożach graniastosłupa. Jest to najmniejsza jednostka przestrzenna, z której wychodząc można zbudować nieskończony zbiór okresowy przez układanie obok siebie identycznych graniastosłupów bez pozostawiania między nimi miejsc pustych. Przeciwnie, jeżeli występują dodatkowe węzły we wnętrzu graniastosłupa, na jego ścianach lub krawędziach, to komórkę nazywamy komórką wielokrotną. Należy pamiętać, że wszystkie węzły sieci są punktami równoważnymi. W związku z tym każdej

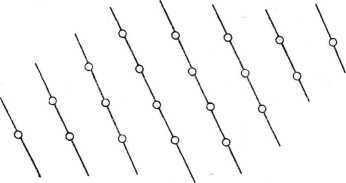
Rys. 1.30. Rodzina prostych sieciowych

54