61337 Str012 (2)

20 I. Kilka ngadniett elementarnej teorii licab

inne szczegóły administracyjne, takie jak czas potrzebny do porównania dwóch liczb zapisanych w systemie dwójkowym (tzn. do wzięcia akurat tylu bitów dzielnej, by otrzymana liczba całkowita była większa od dzielnika), do przeniesienia cyfr itp. Zatem naszym oszacowaniem jest po prostu (k — l + 1)1, co z kolei jest mniejsze od kl.

Przykład 8. Znajdźmy ograniczenie górne liczby operacji na bitach potrzeb-

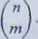
nych do obliczenia współczynnika dwumianowego

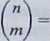
założyć, że m < «/2. Wykorzystajmy do obliczenia następujący wzór:

= n(n — l)(n — 2)...(n — m + 1)1(2 • 3 • ... • ni). Mamy tu m — 1 mnożeń, po których następuje m — 1 dzieleń. W każdym z tych dziaiań największą możliwą wielkością pierwszej liczby jest n(n — l)(n — 2)... (n — m + 1) < n^m, a ograniczeniem drugiej liczby jest n. Na podstawie takiego samego rozumowania jak w rozwiązaniu przykładu 6 otrzymujemy, że ograniczeniem liczby wszystkich operacji na bitach jest 2(m — l)/w([log₂ ń\ + l)², co dla dużych min jest w przybliżeniu równe 2m²(Iog₂n)².

Wprowadzimy teraz bardzo wygodne oznaczenie pozwalające na podsumowanie powyższych rozważań dotyczących oszacowania czasu.

Notacja O. Przypuśćmy, że f(ń) i g(n) są funkcjami zmiennej naturalnej n o wartościach dodatnich (niekoniecznie całkowitych). Mówimy, że f(ń) = 0(g(n)) (lub po prostu, że /= O(g)), jeżeli istnieje stała C taka, że wartość f(n) jest zawsze mniejsza od C • g(n). Na przykład 2n² + 3 n — — 3 = 0(n²) (bowiem nietrudno dowieść, że lewa strona jest zawsze mniejsza od 3n²).

Ponieważ chcemy używać notacji O w ogólniejszych sytuacjach, przyjmiemy definicję mającą szersze zastosowania. Mianowicie dopuścimy funkcje fi g wielu zmiennych i nie będziemy zajmować się relacjami pomiędzy fig dla małych wartości argumentu n. Podobnie jak przy badaniu granic dla n -* oo w analizie matematycznej, będziemy zainteresowani wyłącznie dużymi wartościami n.

Definicja. Niech f(n_it n_2i ..., n_r) i g(n_l9 n₂, ..., n_r) będą dwiema funkcjami, których dziedzinami są podzbiory zbioru wszystkich ciągów r-wyrazowych liczb całkowitych dodatnich. Przypuśćmy, że istnieją takie dwie stałe B i C, że jeśli tylko wszystkie n_} są większe od B, tp obie funkcje są określone, mają wartości dodatnie oraz f(n_it n₂,n_r) < Cg(n_L, n₂,..., n_r). W takim przypadku mówimy, że funkcja/jest ograniczona przez g i piszemy f = 0(g).

Zauważmy, żc relacja „ - ” w notacji O powinna być traktowana bardziej jak a o samym O powinniśmy myśleć jak o „pewnej stałej multy-plikatywnej”.

Przykład 9.

(a)    Niech f(n) będzie dowolnym wielomianem stopnia d mającym dodatni współczynnik przy najwyższej potędze niewiadomej. Wtedy łatwo dowieść, że/(») = 0(tć). Ogólniej, można dowieść, źe/= O(g), jeśli tylko istnieje skończona granica f(n)/g(n) przy n -* oo.

(b)    Jeśli e jest dowolnie małą liczbą dodatnią, to można dowieść, że log/i = = 0(n*) (tzn. dla dużych n wartości funkcji log są mniejsze od wartości dowolnej funkcji potęgowej, niezależnie od tego jak mały jest wykładnik

log/z

= 0, czego można dowieść za po

potęgi). Wynika to z tego, że lim

H-tt "

mocą reguły de 1’Hospitala.

(c)    Jeśli f(ń) oznacza liczbę k cyfr dwójkowych liczby n, to z powyższych wzorów wynika, że f(n) = 0(1 ogn). Zauważmy też, że tę samą zależność otrzymamy dla liczb zapisanych w dowolnym innym systemie pozycyjnym o ustalonej podstawie b. Z drugiej strony przypuśćmy, że pozwolimy również rosnąć podstawie b i przez/(«, b) oznaczymy liczbę cyfr liczby n przy podstawie b. W takim przypadku będziemy korzystać z oszacowania

lilii    |

(d)    Mamy: Czas(n * m) = 0(logn • logm), gdzie lewa strona oznacza liczbę operacji na bitach potrzebnych do pomnożenia liczby n przez liczbę m.

(e)    W przykładzie 6 możemy napisać:

Czas(n!) = 0((n logn)²).

(f) W przykładzie 7 mamy:

Czas^a^ • Ibjd) = ©(/^^((logm)²! + log(min(«_t, Hj)))).

W naszych zastosowaniach funkcje f(n) i /(n_£, n₂, ..., n,) będą często oznaczać ilość czasu potrzebnego do wykonania pewnego zadania arytmetycznego na liczbie n lub na liczbach n_£, n₂,..., n_r. Chcemy znaleźć możliwie prostą funkcję g(n) jako nasze ograniczenie. Jednakże nie chcemy otrzymać funkcji g(n) przyjmujących wartości dużo większe niż jest to potrzebne, gdyż prowadzi to do przesadnego wyobrażenia o czasie wykonania danego zadania (chociaż ze ściśle matematycznego punktu widzenia poprawne jest zastąpienie w relacji f = O(g) funkcji g(n) funkcją przyjmującą większe wartości).

Z grubsza rzecz biorąc, relaq'a/(n) = 0(n^d) oznacza, że funkcja/rośnie w przybliżeniu tak szybko jak d-ta potęga zmiennej n. Jeśli na przykład d — 3, to ta relacja oznacza, że podwojenie zmiennej n da w wyniku mniej więcej