34035 Str021 (2)

38 I. Kilka rnpdnicrt elementarnej teorii liczb

0 i rnrt - I, < 11:t której j ts /, (mod m) oraz jj₂ (mod ń). Zauważmy, źc j nic ma wspólnego dzielnika z mn wtedy i tylko wtedy, gdy nie ma wspólnego dzielnika im co jest równoważne temu, źc j\ nic ma wspólnego dzielnika z m oraz nic ma wspólnego dzielnika z n- co jest równoważne temu, że j₂ nie ma wspólnego dzielnika z n. Zatem te liczby j_% które musimy zliczyć, odpowiadają wzajemnie jednoznacznie parom j_l%j₂, dla których 0    < m, NWD(J_U

w) - I; 0    < n, NWD{j_1% n) = I. Liczba takich j\ jest równa ę(tn) i liczba

takich j₂ jest równa q>(n). Zatem liczba par jest równa (p(m)q>(n). To kończy dowód wniosku.

Ponieważ każda liczba n może być przedstawiona jako iloczyn potęg liczb pierwszych i każda taka potęga jest względnie pierwsza z pozostałymi,

więc ze wzoru ę>(/?*) = p^a^\--J i z powyższego wniosku wynika, że dla

liczby n = p*t pf⁵ ~.Pr^r mamy

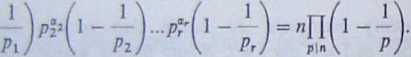
<p(n)=p*i

Wnioskiem z powyższego wzoru na ę(ń) jest następujące twierdzenie, z którego skorzystamy, gdy będziemy omawiać system kryptograficzny RSA z publicznym kluczem.

Twierdzenie 13.4. Przypuśćmy, że o liczbie całkowitej n wiadomo, że jest ona iloczynem dwóch różnych liczb pierwszych. Wtedy znajomość obu czynników pierwszych p i q jest równoważna znajomości q>(n). Dokładniej, wartość '*») można wyznaczyć z p i q za pomocą O(logn) operacji na bitach oraz oba ^_t_. niki p i q można wyznaczyć z ni <p(ń) za pomocą 0(log³n) operacji na bitach.

Dowód. Twierdzenie jest trywialne, jeśli liczba n jest parzysta, gdyż w tym przypadku od razu wiemy, że p = 2, q = n/2 i q>(n) = n/2 — 1; możemy więc założyć, że liczba n jest nieparzysta. Z multyplikatywności funkcji q> dla n = pq mamy q>(n) = {p — 1 )(q— 1) = n 4- I — (p + q). Zatem wartość q>(n) można obliczyć z p i q, wykonując jedno dodawanie i jedno odejmowanie. Na odwrót, przypuśćmy, że znamy n i <p(/i), ale nie znamy p i q. Będziemy traktować p i q jako niewiadome. Znamy ich iloczyn n oraz ich sumę, ponieważ p + q = = n + 1 — q>(ń). Oznaczmy prawą stronę przez 2b (zauważmy, że jest ona parzysta). Ale dwie liczby, których suma jest równa Ib i których iloczyn jest równy n, są pierwiastkami równania kwadratowego x² — 2bx + n = 0. Zatem p i q są równe b ± yfb¹ — n . Najbardziej czasochłonną czynnością jest tu obliczenie pierwiastka kwadratowego, ale z ćwiczenia 12 w podrozdziale 1.1 wynika, że można go obliczyć za pomocą 0(log³n) operacji na bitach. To kończy dowód twierdzenia.

1.3. Kongrnencje 39

Z kolei zajmiemy się uogólnieniem małego twierdzenia Fermata, pochodzącym od Eulera.

Twierdzenie 1.3.5. Jeśli NWD(a, m) = i, /o a**' = 1 (mod m).

Dowód. Najpierw udowodnimy twierdzenie w przypadku, gdy liczba m jest potęgą liczby pierwszej; m = jf. Zastosujemy indukcję względem a. Przypadek a = I jest dokładnie małym twierdzeniem Fermata (twierdzenie 1,3.2). Przypuśćmy, że a ^ 2 i wzór jest prawdziwy dla fP~^l. Wtedy a? ^I_p*”^a = 1 +jf~^lb dla pewnej liczby całkowitej b, na podstawie założenia indukcyjnego. Podnosząc obie strony równości do potęgi p i korzystając z tego, że współczynniki Newtona w rozwinięciu (1 + x)P są podzielne przez p (z wyjątkiem 1 i współczynnika przy x^p na końcu), stwierdzamy, że liczba af ' jest sumą liczby 1 i pewnej liczby składników podzielnych przez p*. Zatem liczba a^9{p0) — 1 jest podzielna przez fP, co dowodzi twierdzenia dla potęg liczb pierwszych.

Wreszcie, z multyplikatywności funkcji <p wynika, że a*^-0 s 1 (mod pP) (wystarczy po prostu podnieść obie strony kongruencji a**⁰* = 1 (mod pf) do odpowiedniej potęgi). Ponieważ jest to prawdziwe dla każdej potęgi p“j|m i ponieważ potęgi dwóch różnych liczb pierwszych nie mają wspólnego dzielnika, z własności 5 kongruencji wynika, że a*'"⁾ = 1 (mod ni).

Wniosek. Jeśli NWD(a, m)= 1 z jeśli ri jest resztą z dzielenia n przez (p(m), to cP = aⁿ' (mod m).

Ten wniosek może być udowodniony w taki sam sposób jak wniosek z twierdzenia 1.3.2.

Uwaga. Z dowodu twierdzenia 1.3.5 wynika, że istnieje niższa potęga liczby a przystająca do 1 modulo m, mianowicie najmniejsza wspólna wielokrotność wykładników potęg przystających do 1 modulo jp dla wszystkich jP\\m. Na przykład a¹² = 1 (mod 105) dla a względnie pierwszych z liczbą 105, ponieważ 12 jest wielokrotnością 3—1, 5 — 1 i 7—1. Zauważmy przy tym, że <p(105) = 48. A oto następny przykład:

Przykład 3. Obliczmy 2^1000000 modulo 77.

Rozwiązanie. Ponieważ 30 jest najmniejszą wspólną wielokrotnością liczb <p(7) = 6 i (p(\ 1) = 10, więc z powyższej uwagi otrzymujemy 2³⁰ = 1 (mod 77). Ponieważ 1000000 =» 30 • 33333 + 10, więc 2^1000000 s 2¹⁰ = 23 (mod 77). Inna metoda rozwiązania polega na obliczeniu najpierw 2^1000000 modulo 7 (ponieważ 1000000 — 6 • 166666 + 4, więc w wyniku otrzymamy 2* = 2), potem 2ioooooo _mo{juio 11 (ponieważ 1000000 dzieli się przez 11 — 1, więc w wyniku otrzymamy 1), a następnie skorzystaniu z chińskiego twierdzenia o resztach, by znaleźć liczbę x zawartą między 0 i 76, która przystaje do 2 modulo 7 i do 1 modulo 11.