str038 (5)

38 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

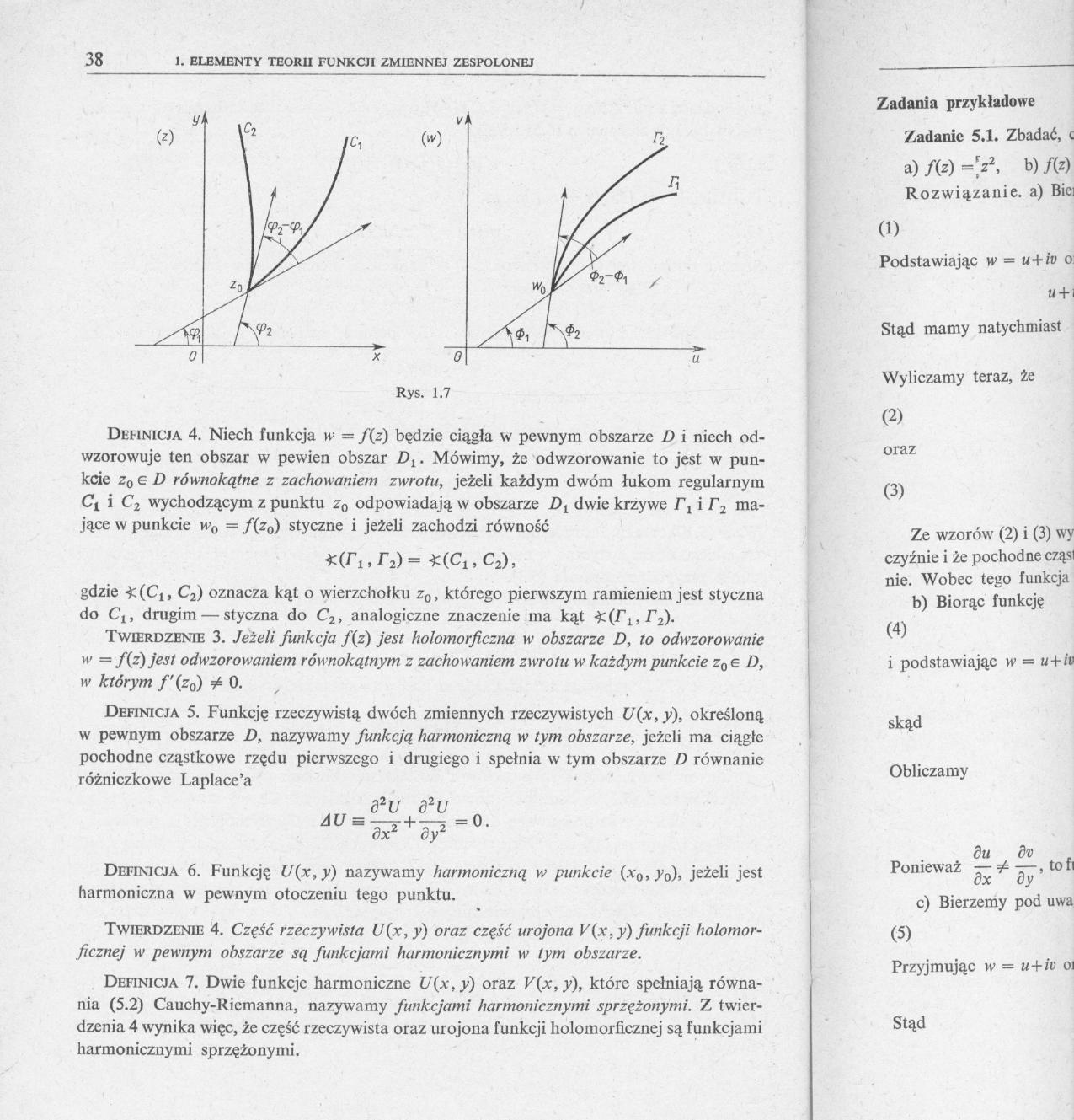
Definicja 4. Niech funkcja w = /(z) będzie ciągła w pewnym obszarze D i niech odwzorowuje ten obszar w pewien obszar Dj. Mówimy, że odwzorowanie to jest w punkcie z₀e D równokątne z zachowaniem zwrotu, jeżeli każdym dwóm lukom regularnym C_t i C₂ wychodzącym z punktu z₀ odpowiadają w obszarze D_t dwie krzywe F, i r₂ mające w punkcie w₀ = /(z₀) styczne i jeżeli zachodzi równość

gdzie    C₂) oznacza kąt o wierzchołku z₀, którego pierwszym ramieniem jest styczna

do C,, drugim — styczna do C₂, analogiczne znaczenie ma kąt ■^(r₁,r₂).

Twierdzenie 3. Jeżeli funkcja /(z) jest holomorficzna w obszarze D, to odwzorowanie w = /(z) jest odwzorowaniem równokątnym z zachowaniem zwrotu w każdym punkcie z₀ e D, w którym f'(z₀) # 0.

Definicja 5. Funkcję rzeczywistą dwóch zmiennych rzeczywistych U(x,y), określoną w pewnym obszarze D, nazywamy funkcją harmoniczną w tym obszarze, jeżeli ma ciągłe pochodne cząstkowe rzędu pierwszego i drugiego i spełnia w tym obszarze D równanie różniczkowe Laplace’a

d²U d²U ^AU = ~dx²+dy²

Definicja 6. Funkcję U(x, y) nazywamy harmoniczną w punkcie (x₀, _f₀), jeżeli jest harmoniczna w pewnym otoczeniu tego punktu.

Twierdzenie 4. Część rzeczywista U(x, j>) oraz część urojona V(x, y) funkcji holomorficznej w pewnym obszarze są funkcjami harmonicznymi w tym obszarze.

Definicja 7. Dwie funkcje harmoniczne U(x,y) oraz V(x,y), które spełniają równania (5.2) Cauchy-Riemanna, nazywamy funkcjami harmonicznymi sprzężonymi. Z twierdzenia 4 wynika więc, że część rzeczywista oraz urojona funkcji holomorficznej są funkcjami harmonicznymi sprzężonymi.