75799 str120 (5)

120 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

dwóch cięć (rys. 1.44), homografia co =

T+

TS

odwzorowuje obszar zakreskowany na ry

sunku 1.44 na płaszczyznę zmiennej (co) wzdłuż cięcia, które jest półosią rzeczywistą dodatnią (rys. 1.45). Funkcja w = \[<o odwzorowuje płaszczyznę zmiennej (co) bez półosi rzeczywistej dodatniej w górną półpłaszczyznę.

z +1

Wskazówka: funkcja homograficzna £ =- przekształca śred-

z— 1

nicę AC (rys. 1.42) w tę półoś rzeczywistą, która zawiera obraz punktu z = 0, a więc punkt £ = — 1, tzn. na półoś rzeczywistą ujemną. Póło krąg A DC przechodzi przy homografu z+1

£ =-- w tę półprostą, która jest prostopadła do osi rzeczywistej (odwzorowanie jest

z— 1

bowiem konforemne) i zawiera obraz punktu z = i, a więc punkt £ = —tzn. na półoś

i°.». - (£j).

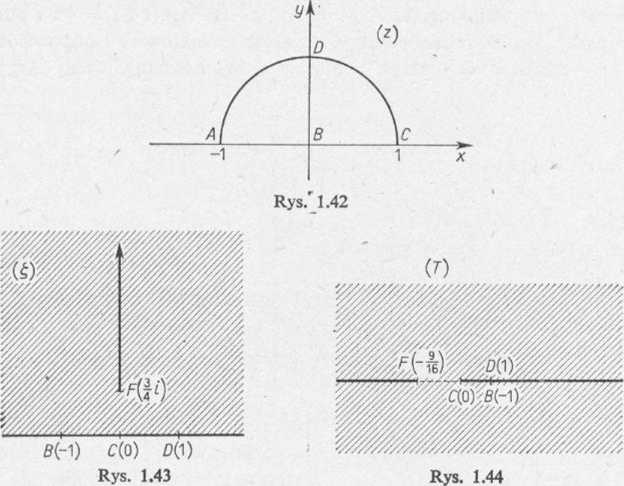
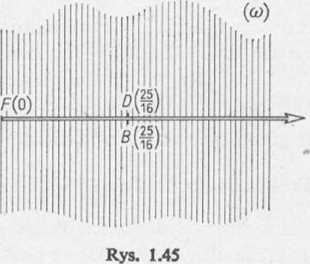
urojoną ujemną. Obszar otrz; mamy Jt<arg£<-§7t; funkcja górną półpłaszczyznę zmieni

11. w =

/lii . Wskaż V z— 1

czyźnie (z) w płaszczyznę z funkcja T = Vę odwzorowuj' niej w górną półpłaszczyznę.

12. w

/g— (1+0 _w

V (2+20-2

13.    Na całą płaszczyznę i rzeczywistej.

14.    Proste zawarte w pasi okręgów

ograniczone punktami ±i. 0 chodzą w okręgi

pozbawione jednego punktu ! W szczególności oś urojona + /, — i, natomiast odcinek -wistą Ou.

y

a'<	0	)
2			c

4z+1

15.    w =-, R = 2.

z+4

1    2z—3 + i

16. w = -=---—r ■

y[2 z—2 + 1

z, = i (3 + 0, z₂ = (2+1).