str042 (5)

42 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ
Wyznaczyć składowe Kx i Ky wektora natężenia rozważanego płaskiego pola elektrostatycznego wiedząc, że wektor K w postaci zespolonej określony jest następującym wzorem:
K = Kx + iKy = -i w'(z).
Rozwiązanie. Obliczamy pochodną funkcji w(z)
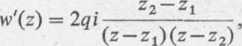
skąd po dokonaniu odpowiednich przekształceń mamy
w



Mając na uwadze, że K = —iw'(z), możemy obecnie napisać wzory określające składowe Kx i Ky natężenia pola
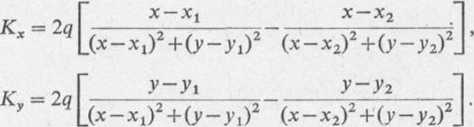
Zadanie 5.4. Wyznaczyć potencjał zespolony pola elektrostatycznego wytworzonego przez dipol punktowy o momencie p umieszczony w punkcie z, = 0 oraz wektor natężenia tego pola.
Rozwiązanie. Potencjał zespolony układu dwóch elektrycznych różnoimiennych ładunków ±q umieszczonych w punktach z, = 0 i z2 = —k (A:>0) wyraża się wzorem
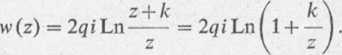
Jeżeli w powyższym wyrażeniu uwzględnimy fakt, że moment danego układu ładunków p — qk, to otrzymamy
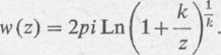
Obecnie wyznaczamy granicę funkcji w>(z) dla k-*0, przy założeniu, że p = qk = const. W granicy otrzymujemy potencjał zespolony F(z) punktowego dipolu elektrycznego o momencie p umieszczonego w początku układu współrzędnych
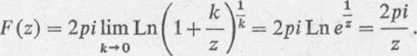
Wyszukiwarka
Podobne podstrony:
str008 (5) 8 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Z wyrazów ciągu (1.4) tworzymy nowy ciąg
str024 (5) 24 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Stąd po przekształceniach dla a 0 mamy(
str050 (5) 50 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zauważmy teraz, że na O A = Jt mamy z =
20159 str096 (5) 96 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ 96 1. ELEMENTY TEORII FUNKCJI ZMI
75799 str120 (5) 120 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ dwóch cięć (rys. 1.44), homograf
79652 str018 (5) 18 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Zadanie 2.7. Przez powierzchnię p
83008 str052 (5) 52 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ 88 52 1. ELEMENTY TEORII FUN
str012 (5) 12 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ Funkcja zespolona zmiennej rzeczywistej
str028 (5) 28 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ (4.10) e2 + 2*!ti _ gZ ^ (4.11) sin (z
więcej podobnych podstron