61395 skan0001 (15)

46

Rozwiązanie ogólne określa wyrażenie:

y² *    . z³ _n

y+ ysms~ —==C.

Wyznaczyć całki ogólne równań różniczkowych:

2.    (y²x - y³)dx + (1 - y²x)dy = 0

3.    ydx + x(x²y — 1 )dy — 0

2. Łatwo stwierdzić, że nie jest to równanie zupełne, gdyż

M_y = 2yx — 3y², N_x = — y², a więc M_y ± N_x.

Szukamy czynnika całkującego. Zauważmy, że wyrażenie

M_y - N_x _ 2y{x — y)

N 1 — y^x

nie jest funkcją tylko zmiennej x, więc nie istnieje czynnik całkujący n = Ponieważ wyrażenie

My-N_x = 2y{y - x) _    2 ₌

M y²(a;-y) y ^KV)

jest funkcją tylko zmiennej y, więc czynnik całkujący istnieje i ma postać:

n = ef(~»)^dv A y²

Mnożymy obie strony równania wyjściowego przez czynnik całkujący, więc (a; — y)dx + (y~² — x)dy = 0.

Otrzymane równanie jest równaniem zupełnym. Rozwiązując je, mamy:

mm o / x

u_x=x-y, więc u == -x - xy + <p(y).

Stąd

u_v = -x + <p'(y) = y ² - x, czyli ip'{y) = y~*. Całkując (fi¹ względom ?/, mamy

__Eto) ■-irlA.fli. ..............

a więc całka ogólna jest opisana wzorem:

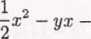
1

- = C. V

3. Łatwo sprawdzić, że nie istnieją czynniki całkujące zależne tylko od jednej zmiennej x lub y. Szukamy czynnika całkującego w postaci = x^py^q. Mnożąc równanie przez funkcję fi, otrzymujemy

(2.5.7)

x^py^q+1dx + (x^p+3y^q+1 - x^p+1y^q)dy = 0.

Przyjmujemy oznaczenie

M* (x, y) = x^py^q+1,    N*(x,y) = x^p+3y^q+1 - x^p+1y^q

i wyznaczamy

M_v* = (q + iyy, K = (p + 3)x^y“+¹- - (p ^PyK-

Łatwo zauważyć, że otrzymane równanie będzie równaniem zupełnym wtedy i tylko wtedy, gdy M* = N*. Stąd, porównując współczynniki przy wyrażeniach: WW oraz x^p+2y^q+1, otrzymamy następujący układ równań

q + 1 = ~{p + 1) 0 = p + 3.

Oczywiście q = 1, p = — 3 jest rozwiązaniem tego układu, a więc

H{x,y) = aT³y

Jest szukanym czynnikiem całkującym i równanie zupełne (2.5.7) ma postać:

(2.5.8)

x ³y²dx + (y² - x~²y)dy = 0.

ll u/,wiązując to równanie, mamy:

u_x = x y,

Uąd wynika, że całka ogólna jest dana wzorem