62533 MATEMATYKA156

302 VI. Ciągi i szeregi funkcyjne

Warunek wystarczający jednostajnej zbieżności SZEREGU FUNKCYJNEGO

KRYTERIUM WEIERSTRASSA. Jeżeli dla każdego x g X i każdego n eN spełniony jesi warunek

*1    «c

oraz szereg liczbowy £a„ jest zbieżny, to szereg ftinkcyjny £f_n(x) jest

»■!    Bfl

jednostajnie i bezwzględnie zbieżny na zbiorze X,

Inaczej. Jeżeli dla szeregu funkcyjnego istnieje tui zbiorą: X maj nru □ ta liczbowa zbieżna, to szereg ten jest jednostajnie i bezwzględnie zbieżny na zbiorze X

Twierdzenie pozostaje prawdziwe, gdy nierówność (2.1) spełniona jest od pewnego numeru n począwszy.

PRZYKŁAD 2.2 Korzystając z kryterium Wcierstrassa wykażemy jednostajną i bezwzględną zbieżność szeregów na wskazanym zbiorze X.

a) Szereg geometryczny £xⁿ jest jednostajnie i bezwzględnie zbieżny na każdym przedziale domkniętym <-a,a>, gdy 0<a<l. ponieważ dla każdego x e< a,a> i neN mamy |xⁿ|<a‘ oraz szereg liczbowy £aⁿ jest zbieżny (geometryczny o ilorazie a c(0,l)).

b) Szereg

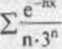
jest jednostajnie i bezwzględnie zbieżny na

przedziale < 0, -ł-oc), gdyż

^^d,a x €<0,+oo), neN ni n-3

oraz szereg Y—- jest zbieżny (np. kryterium Cauchv'ego).

n-3

c) Szereg £-ⁿ-^ jest jcdnosiaimc i bezwzględnie zbieżny na n

zbiorze R. gdyż

I— j— l^s_T dla x eR, neN n n‘

oraz szereg jest zbieżny (harmoniczny rzędu et = 2).    ■

Całkowanie i różniczkowanie szeregu funkcyjnego

TWIERDZENIE 2.1 Jeżeli szereg funkcyjny £f_n(x) funkcji

n»l

ciągłych na przedziale domkniętym <a,b> jest jednostajnie zbieżny na

</> h

tym przedziale i jego suma jest równa f(x), to szereg £jf_n(x)dx jest

ił-i*

zbieżny i jego suma jest równa jf(x)dx, czyli

(ZW = «*»=* <ŹJ f„(x)dx = J f(x)dx).

n«)    n=l a    ą

Mówimy \v1edy. Ze szereg funkcyjny można całkować wyraz po wy razić.

TWIERDZENIE 2.2 Jeżeli szereg funkcyjny £f_n(x) funkcji

l\=1

różmczkowalnych na przedziale domkniętym < a,b > jest zbieżny na tym

•*>

przedziale i jego suma jest równa f(x) oraz szereg pochodnych £f_n'(x)

n 1

oo

jest jednostajnie zbieżny na tym przedziale, to szereg pochodnych £f_n'(x) ma sumę równą f'(x) na tym przedziale, czyli

n-1    na)

Mówimy wlekły, że szereg funkcyjny moma różniczkować wyraz po wyrazie ZADANIA DO ROZWIĄZANIA

1. Wyznaczyć zbiór tych x, dla których dany szereg geometryczny jest zbieżny oraz obliczyć sumę tego szeregu:

Jc*) i/²⁰"¹.    b)£x²ⁿ-\    j-c) +

nO

n*l

n I n=l