62970 Untitled Scanned 71

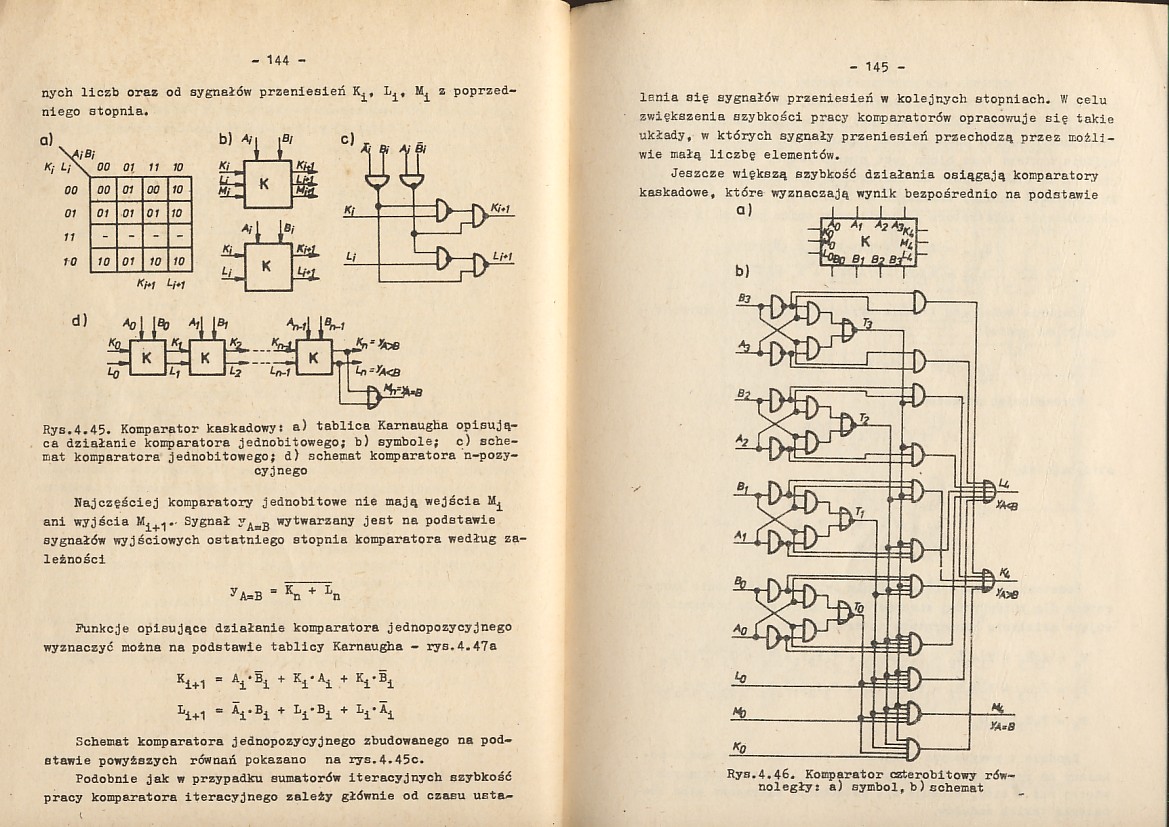
nych liczb oraz od sygnałów przeniesień K_if L^, z poprzedniego stopnia.

00 01 11 10

00	01	00	10
01	01	01	10
-	-	-	-
10	01	10	w

a)

l i Bi

Ki ^ 00 01 11 10

Kf*1 i-M

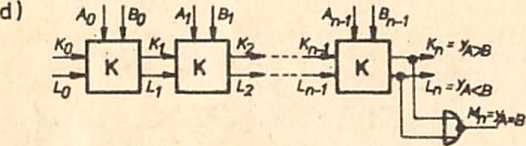
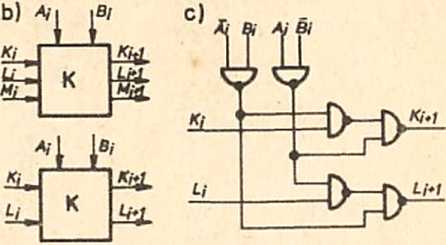
Rys.4.45. Komparator kaskadowy: a) tablica Karnaugha opisująca działanie komparatora Jednobitowego; b) symbole; c) schemat komparatora jednobitowego; d) schemat komparatora n-pozy-

cyjnego

Najczęściej komparatory Jednobitowe nie mają wejścia ani wyjścia    Sygnał y_ArłB wytwarzany Jest na podstawie

sygnałów wyjściowych ostatniego stopnia komparatora według zależności

^AaB ” ^Kn ^{+ Ł}n

Funkcje opisujące działanie komparatora jednopozycyjnego wyznaczyć można na podstawie tablicy Karnaugha - rys.A.47a

^Ki₊1 * V⁵i ^{+ K}i‘^Ai ⁺ V⁵i

^Li+1 ^{= A}i*^Bi ^{+ L}i’^Bi ^{+ L}i’^Ai

Schemat komparatora jednopozycyjnego zbudowanego na podstawie powyższych równań pokazano na rys.4.45c.

Podobnie Jak w przypadku sumatorów iteracyjnych szybkość pracy komparatora iteracyjnego zależy głównie od czasu ustalenia się sygnałów przeniesień w kolejnych stopniach. W celu zwiększenia szybkości pracy komparatorów opracowuje się takie układy, w których sygnały przeniesień przechodzą przez możliwie małą liczbę elementów.

Jeszcze większą szybkość działania osiągają komparatory kaskadowe, które wyznaczają wynik bezpośrednio na podstawie

-l. „1-1

^A1 ^A2 ^a3.

K

^ Bi fl? Bj*

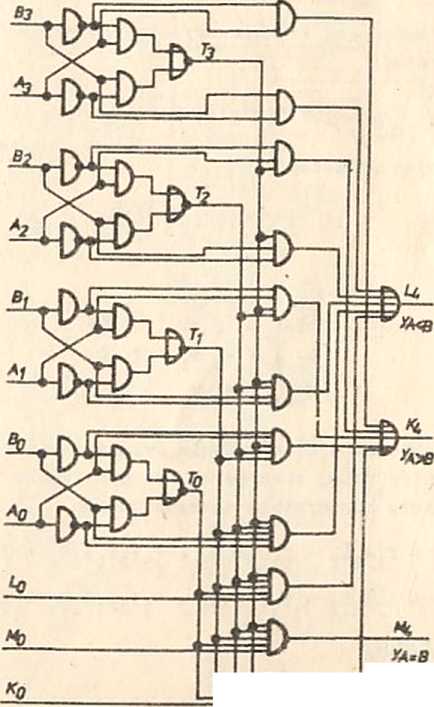
b)

Rys.4.46. Komparator czterobitowy równoległy: a) symbol, b) schemat