63934 PC043376

fj Uwaga 1.25. istnieją funkcje, które nie są ani parzyste, ani nieparzystej przykład 1,59).

Ponieważ istnieje tylko jedna funkcjaf(x)-0, która jest jednocześnie par> sta i nieparzysta, jeżeli badana funkcja okaże się parzysta, na pewno nie będ^ ona nieparzysta (o ile nie jest funkcją stale równą 0).

1.4.5. Okresowość funkcji

Definicja 1.50. Funkcję y = f(x) nazywamy okresową, gdy istnieje talu liczba T > 0, że dla każdego xe D_f również x+Te Dj i x-Te D_f oraz fU) =/(r + T) =f(x - T), tzn.

SSfllllB P11S    tff

(por. ilustracja 1.23).

Ilustracja 1.23. Wykres funkcji okresowej

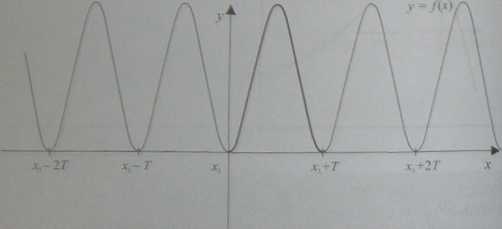
i Dowolną liczbę T spełniającą warunki określone w definicji 1.50 nazywani) okresem funkcji /. Najmniejszą z nich (o ile istnieje) nazywamy okresem podstawowym funkcji/.

Przykład 1.60

Klasycznymi przykładami funkcji okresowych są znane ze szkoły średniej funkcje trygonometryczne. Wiemy, że funkcje sin x i cos * są funkcjami o okresie podstawowym 2it:

V sinx = sin(x+27i), V cosjc=cos(jc+2jt),

xeR

a funkcje tgjc oraz ctgjc są funkcjami o okresie podstawowym n:

V

xeR\[4f-+*n}

tgx = tg(x+7t),

V

VjKR\{fc*}

CtgX = Ctg(* + Jt).

Pozostałe własności funkcji trygonometrycznych omówimy w podrozdziale

1.6.8.

1.4.6. Monotoniczność funkcji. Ekstrema lokalne funkcji

W ekonomii ważnym zagadnieniem jest badanie tendencji pewnych zjawisk. Inwestorzy giełdowi, śledząc sprawozdania finansowe, zwracają uwagę na to, czy zysk spółek rośnie, czy maleje.

Definicja 1.51

a)    Funkcję/: X —>Ynazywamy rosnącą w zbiorze (przedziale) A c X, jeżeli dla każdej pary argumentów x,. x₂e A z nierówności x, < x, wynika nierówność/(x,) </(xb), tzn.

V    Fx. <x, => /(x₁)</(x₂)l (por. ilustracja 04).

jtl.jrjeA¹-    V:.':

b)    Funkcję f:X-*Y nazywamy malejącą w zbiorze A a X. jeżefi cBa każ

dej paty argumentów a . x₂e A z nierówności x, <x₂ wynika mc\(mac6Ł /(x_t)>/^2),tzn.    |

V    fx, < x₂ => f(xi V> /(x, VJ (por. ilustracja 125).

-* -.,_v; .•

c)    Funkcję/:^ -* Ynazywamy stalą w zbiorze ^ cl, jeżeli istnieje c e K, takie, że dla każdegoxe A,f(x)=c₇ tzn.

pi V /(x)=c (por. ilustracja 1.26).

Powyższe definicje można również ująć mniej formalnie.