68317 new 77 (2)

156 7. Zasady obliczeń wytrzymałościowych śrub

na odcinku l_b. Śruba pod działaniem siły Q_r również jest rozciągana. Z rysunku 7.33b wynika, że

h + Ak = (l_a-Al_a)+(l_b+Al_b)+(l_c-Al_c),    (7.78)

a ponieważ długość śruby h = l_a+l_b+l_c, więc

Ah+Al_a+Al_c = Al_b.    (7.79)

Przyjmijmy, że część obciążenia roboczego wywołująca rozciąganie tulei na odcinku l_b jest równa X (rys. 7.33c). Wydłużenie tego odcinka jest równe

Al_b = X-±- = Xh.    (7.80)

tzt¹ b

gdzie E₂ jest modułem sprężystości materiału tulei. Wówczas siła ściskająca tuleje na odcinkach l_a i Z_c, a także siła rozciągająca śrubę (patrz rys. 7.33c) wynosi Q_r—X, a odkształcenia wspomnianych odcinków tulei i śruby są odpowiednio równe

Al_a = (Q_r-X)^-= (Q_r-X)ż„

Al_c — (Q_r~X)

lc

e₂f

2* c

(Qr-X)/._c

(7.81)

Ali — (Qr~X)

E]F i

(Qr-X);.!.

Podstawiając (7.80) i (7.81) do (7.79) wyznaczymy siłę rozciągającą tuleję na odcinku l_b

X = Q_r

(7.82)

l_a + Ż_c + ii

/._a+/._b + l_c + ii ’

stąd obciążenie rozciągające śrubę

Q-X = Q_r-

(7.83)

il + i-2 ’

gdzie i₂ = Afl-hAb+ic — podatność tulei.

Jeśli układ jak na rys. 7.33 jest wstępnie obciążony siłą Q_w, to całkowite obciążenie śruby zgodnie z zasadą superpozycji wyraża wzór

Qc - Qw+Q_r -

Qw+xQr-

(7.84)

Z taką samą siłą ściskana jest tuleja na odcinkach l_a i l_e. Natomiast na odcinku l_b tuleja ściskana jest siłą

Należy zwrócić uwagę, że współczynnik obciążenia roboczego śruby X jest określony przez stosunek podatności rozciąganego odcinka tulei do sumy podatności wszystkich elementów układu. Wartość tego współczynnika zawierać się może w przedziale od % = 0 dla l_b = 0 do x ⁼——

Ji + ż₂

dla l_b = li.

Jeśli x — 0» to dla dowolnie dużego obciążenia roboczego Q_r (również zmiennego w czasie) — obciążenie śruby nie ulega zmianie (Q_c = Q_w), a o wytrzymałości tego modelowego układu decyduje warunek rozcdąga-nia-ściskania tulei przy naprężeniu maksymalnym

(7.86)

Qr Q li

minimalnym

0min

Qu

(7.87)

Zastąpienie jednolitej tulei kilkoma elementami tak jak na rys. 7.33d nie wywołuje zmiany stanu obciążeń i odkształceń, pod tym wszakże warunkiem, że obciążenie Q_r nie powoduje powstania luzu między łączonymi elementami układu. Ponieważ zachowanie docisku jest nieodzowne więc wzory (7.84) i (7.85) zachowują swą ważność dla wszelkich układów połączeń wstępnie napiętych, przy czym wzór (7.85) określa siłę zacisku resztkowego. Graficzny obraz obciążeń i odkształceń przedstawia rys. 7.34. Na

rysunku tym linia kreskowa pochylona pod kątem en |tgcti = ^ wyznacza charakterystykę śruby, a linia kreskowa pochylona pod kątem

charakterystykę odciążanego odcinka tulei.

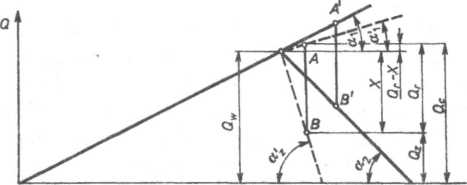
Rys. 7.34. Wpływ miejsca przyłożenia obciążenia roboczego Q_r na charakterystykę obciążeń i odkształceń elementów złącza

Rozpatrzmy obecnie bardziej ogólny przypadek połączenia n elementów (rys. 7.35), w którym po obciążeniu wstępnym Qw przyłożono obciążenie robocze Q_r do elementów j i l. Obciążenie Q_r wywołuje wzrost odkształceń ściskających w elementach od 1 do j-1 i w elementach od Z+l do n oraz zmniejszenie odkształceń w elementach od j do I.