70378 PB032281
jest
SZeregi
em
'% i ii
%
różne---■
Dla * = 1 otrzymujemy: 1 _ 1 i Si+f2'
145
Qi
1 ~q
2 określenia ciągu za pomocą wzoru rekurencyjnego też wynika, że a, =-•
, Założenie indukcyjne: /» = *
1 k
WĘĘ 1
Tezaindukcyjna: n = k+1
' k+l
Ksj 2'
Dowód:
7 określenia ciągu za pomocą wzoru rekurencyjnego mamy:
HIi|
°k*\'k(k + 2) I
k
Podstawiając a* (z założenia indukcyjnego), otrzymujemy:
(k + lj2) k ^k +1
fl*+1 ~A:(& + 2) £+1 lljf
■i li Ar+1
Otrzymaliśmy tezę indukcyjną: a*+,
Wobec tego na mocy zasady indukcji matematycznej wynika, że A an =-
1 neN+
b) lim a„ = lim-= lim —
/*-» oo «->co
"+1
0 PRZYKŁAD 2.87
Dany jest ciąg (a„) o wyrazie ogólnym an = Vw +1 - Vh .
a) Wykaż, że ciąg (a„) jest ograniczony.
b) Zbadaj monotoniczność ciągu (a„).
ROZWIĄZANIE
a) Należy wykazać, że V A mś4n+\-Jń<M.
^aalcając a, =V^TT-^. otrzymujemy:
°w =4n+\-.*[Z-(Jn + l-Jn)(Jn + l+Jn) _ n + l-n _ 1
4n +1+4n 4n+t+4n -Jn+l + ^fn
m-ty wyraz
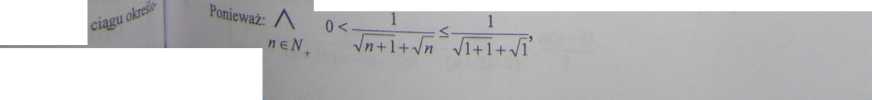
Wyszukiwarka
Podobne podstrony:
125 2 248 XI. Szeregi potęgowe Zadania 249 Dla x — — 1 otrzymujemy 1 11111 (-1)" Jada
MATEMATYKA046 84 II. Ciągi i szeregi liczbowv KRYTERIUM DALEMBERTA (dla szeregów o wyrazach dowolnyc
45 7 2. Jeśli g > 1, to szereg J] a„ jest rozbieżny. Ponadto, jeśli VI I > 1 dla nieskończenie
Podstawą dla zastosowania teom systemów w estetyce jest szereg stanowisk reprezentowanych przez este
Potencjał elektryczny Różnica energii potencjalnych jest dana przeze„-EM.-Fdr A co dla pola
DSCN4002 W U >• uium V tUJ T? 11VŁIVJ p«t-VŁzakwaszanie o Hamujące działanie jonów wodorowych jes
METODOLOGIA BADAŃpraca - definicje Praca jest terminem wieloznacznym i rozmaicie definiowanym - dla
- 48 - I dla furek [ jednokonnych dla furek ii dwukonnych {I
57 Wogóle Jaszczurówka jest miejscem bardzo odpo-wiedniem dla osób, pragnących spokojnego pobytu, tu
img038 (28) badaniu jest dopuszczalne po każdorazowym ustaleniu dla danego betonu poprawek AL wg wzo
img040 (54) Zdaniem Kułakowskiej (1998) autyzm jest spowodowany specyficzną dysfunkcją mózgu, dla kt
więcej podobnych podstron