69851 P1050567 (2)

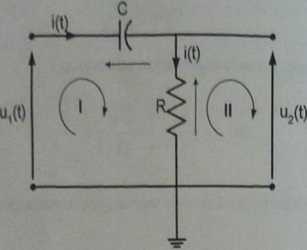
Rys, 3. Schemat badanego układu.

Przeprowadzimy analizę układu przedstawionego na rys. 3. Korzystając z podstawowych praw Kirchhoffi możemy ułożyć równania spadku napięć w oczkach. Równanie oczka pierwszego: i oczka drugiego:

u,(t)=Ri(t).    (10)

Wyznaczymy transformatę Laplace’a równania (9) i (10) przy zerowych warunkach początkowych:

= l(s]

—+R Cs

1+RCs

Cs

Uj(®)⁼I(s)R •

Traiismitancja układu, to stosunek transformaty Laplace’a sygnału wyjściowego do wejściowego przy zerowych warunkach początkowych:

ipgi wi

R

RCs

IW

1+RCs

Cs

1+RCs RCs+l' Cs

(11)

Porównując otrzymaną transmitancję (11) z transmitancją (6), możemy określić stałą czasową układu oraz wzmocnienie członu różniczkującego.

Z charakterystyki skokowej można odczytać:

-    wartość odpowiedzi układu w stanie ustalonym,

-    czas regulacji, który odpowiada przedziałowi czasu od początku symulacji do chwili czasu, gdy odpowiedź przyjmuje wartość z przedziału ±5 % stanu ustalonego.

- wartość maksymalną odpowiedzi układu na wymuszenie, f Miedzy stalą czasową a czasem regulacji występuje stała zależność, która wynosi t,=3,91T. s Korzystając z powyższych zależności można łatwo wyznaczyć parametry układu. Na rys). 4 | przedstawiono odpowiedź rzeczywistego członu różniczkującego, który posiada czas regulacji I równy 3,91 |is, stąd stała czasowa układu wynosi 1 ps oraz wzmocnienie członu w różniczkującego k=0.000001.

Saapn»spona«

%«-• ftNkBflpRudt; t ' Owłiłoot |%): hi

A!*r»(we);0

k

Rys. 4. Odpowiedź układu (dla R= 1 [MO] C=1 [pF]) na wymuszenie skokiem jednostkowym.

Badany	wmw
układ
_ i

Generator

Oscyloskop

Rys. S. Schemat stanowiska laboratoryjnego.