76460 PICT5468 (2)

174 i CIIAlAKTfRYSTYKA MATHUAIÓW ROZDUORNIONYCN

kulistych, które spotyka się najczęściej, porowatość trzeba wyznaczać doświadczalnie. Jedna z metod polega na zalaniu cieczą określonej objętości suchego materiału V. Objętość cieczy wyrównująca się z poziomem materiału suchego odpowiada wolnej objętości V*.

Inna metoda wymaga znajomości gęstości materiału p, i tzw. gęstości usypowej p„. czyli masy przypadającej na jednostkę objętości materiału sypkiego. Masa materiału ziarnistego zajmująca objętość V

«*<M    (M)

Jeżeli płynem wypełniającym wolną objętość zbioru jest powietrze, to można pominąć drugi składnik sumy w równaniu (6.30), a po podzieleniu przez objętość układu uzyskuje się

y ■ - (1 -«)<?.	(631)
	(6 32)

0.

Dla jednakowych cząstek kulistych wyróżnia się górną i dolną granicę porowatości odpowiadającą najluźniejszemu i najściślejszemu upakowaniu złoża. Złoże jest najluźniej upakowane i ma maksymalną porowatość wtedy, gdy środki czterech cząstek wyznaczają kwadrat lub inaczej, gdy jedna warstwa kul znajduje się bezpośrednio nad drugą. Dla takiego ułożenia kul uzyskuje się

0,4765    (633)

0

Złoże jest najściślej upakowane i ma minimalną porowatość wtedy, gdy cząstki tworzą konfigurację romboedryczną. Dla takiej konfiguracji

» 0,2592    (6.34)

W praktyce zauważono, że im cząstki są większe, tym bardziej ich kształt zbliża się do kulistego. W związku z tym większe jest prawdopodobieństwo, że przy normalnym upakowaniu ich porowatość wyniesie 0,26 - 0,47. Im cząstki są mniejsze, tym bardziej odbiegają od kształtu kulistego, zbliżając się do cząstek włók* nistych, iglastych, i tym większe jest prawdopodobieństwo, że ich porowatość będzie przekraczać wartości ekstremalne uzyskane dla kul.

Porowatość nawet jednakowych cząstek kulistych zależy również od odległości od ściany aparatu. Jest ona większa tuż przy ścianie i maleje w kierunku osi aparatu [7]. Wpływ średnicy aparatu na wartość porowatości jest określany często jako tzw. efekt przyidemy. Według Sonntaga i Jeschara średnia porowatość takich warstw [8]

*-* 0.375₊0.m£    (6.35) gdzie - średnica rury.

Ola ceramicznych typowych wypełnień stosowanych w kolumnach do

masy średnie wartości porowatości tm	są następujące:
wypełnienie z kul	0,33 - 0,42
wypełnienie z pierścieniami Raschiga	0.52 - 0.80
wypełnienie z siodełek Berła	0,55 - 0,75
wypełnienie z siodełek Inta!ox	0,65 - 0,85
dla pierścieni Raschiga wykonanych
z cienkiej blachy	>0,9
Porowatość warstwy cząstek o różnych wielkościach jest zawsze mniejsza

od porowatości warstwy składającej się z cząstek jednakowych. Dla złoża składającego się np. z mieszaniny kul o dwóch rozmiarach istnieje zależność [9]

gdzie: V₉₂ — objętość zajęta przez kule mniejsze, V - objętość zajmowana przez kule obu rozmiarów, e - porowatość złoża składającego się tylko z kul dużych albo tylko z małych. Dla przypadku teoretycznego, gdy » 0, zależność tę pokazano na rys. 6.2 jako funkcję V,JV.

różnych średnicach

Rys. 6.3. Wpływ stosunku średnic kuł aa średnią porowatość złoża

Dla V_9J/V - 0 i y₉₂jy - I stosunek gjt % 1. ponieważ w warstwie istnieją wtedy albo tylko kule duże. albo tylko kulki małe. Zwiększając udział małych kul, funkcja przebiega wg krzywej 2, a objętość kul dużych V_9l jest stała do momentu, gdy objętość wolna między dużymi kulami upakowanymi najgęściej będzie całkowicie wypełniona kulkami małymi. Porowatość złoża przyjmuje wtedy wartość najmniejszą ejc = c. Dalszy wzrost wartości powoduje zmianę wartości tjt wzdłuż linii /.

Współrzędne punktu przecięcia krzywej 1 i 2 są następujące:

Dla pszenicy np. e * 0,3, zatem tjt £. - 0,09 [7].

(6-37)

0,3, a stąd minimalna wartość

e

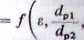
(6.36)