79301 new 75 (2)

152 7. Zasady obliczeń wytrzymałościowych śrub

152 7. Zasady obliczeń wytrzymałościowych śrub

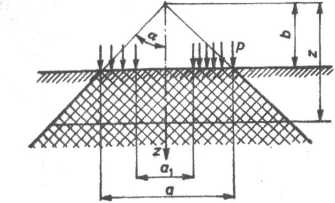
Rys. 7.27. Półprzestrzeń obciążona ciśnieniem kołowosymetrycznym

(7.72)

(' a_z dz    _ p(a² — al) f dz _ p(a² — g*)

.1 E₃    4E₂tg*a ] z¹ ~ 4£₂btg²a

8 0

Obliczając A za pomocą tablic całek eliptycznych z równania (7.70) i podstawiając do równania (7.72) można wyznaczyć |dla różnych— j

wartości tga. Dla = 0-r-0,8 otrzymamy tg a = 0,55-1-0,65, a więc a <

< 45°. W przypadku (istnienia otworu (rys. 7.28) wartości kąta pochylenia tworzącej stożka są jeszcze mniejsze i wynoszą tga — 0,4-r~0,6. W przybliżonych obliczeniach można przyjąć tga = 0,5.

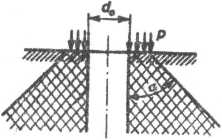
Rys. 7.28. Półprzestrzeń z walcowym wydrążeniem

Naprężenia ściskające w przypadku istnienia otworu o średnicy d_a są równe

a podatność

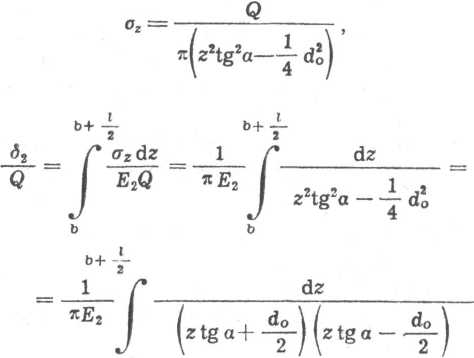
b

Rys. 7.29. Symetryczne stożki obciążeń

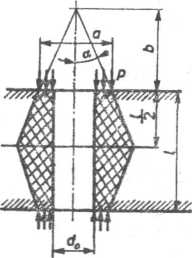
Podstawiając granice całkowania oraz uwzględniając symetryczny stożek obciążenia na przeciwnej powierzchni oporowej (rys. 7.29) otrzymamy

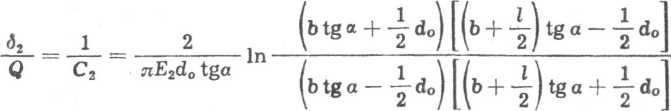
1

(7.73)

Przyjmując zgodnie z rysunkiem btga = a oraz d₀« d (gdzie d jest średnicą śruby) otrzymamy ostatecznie

(7.74)

1 _ d₂ _    2    (a+d) (a + Z tga—d)

Ci Q nE₂dtga ⁿ (a—d) (a + Z tga + d)

W przypadku niejednakowych średnic docisku a_x i a₂ (rys. 7.30) we

a,±aj

wzorze przyjmiemy a —---.

Dla bardzo grubych złącz (I -> oo) powyższy wzór ma postać

Wyrażenie to określa maksymalną możliwą wartość podatności ściskanych elementów; praktycznie stosuje się je przy Z > 20d.

W rzeczywistych układach konstrukcyjnych często występuje taki przypadek, że stożek odkształceń wychodzi poza kontury elementów łączonych (Tys. 7.31). Wtedy podatność określa się zależnością

1

²    _ln(^fl + ^d)(^p~^d) i

E₂jidtga (a~d)(D-\-d)

'2

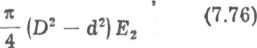
gdzie: