80799 skrypt008

Jego wartość leży w przedziale od -I do 1. Wartość zerowa oznacza brak zależności, natomiast wartość jeden oznacza związek funkcyjny. Należy zwrócić uwagę na interpretację wyników analizy korelacyjnej. Związki przyczynowo-skutkowe są w tym przypadku jednostronne. Wzajemna zależność zmiennych daje duży współczynnik korelacji, natomiast odwrotna nie obowiązuje. Prostą regresji liniowej oraz wartość współczynnika korelacji dla różnych rozkładów punktów pomiarowych pokazano rysunku. 1.2.

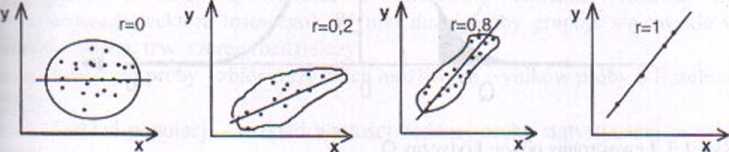
x

Rys. 1.2. Prosta regresji liniowej i współczynnik korelacji rw zależności od usytuowania punktów' pomiarowych

Podobnie jak liniową funkcję regresji, wyznacza się nieliniowe funkcje regresji. Poszerza się jednak zakres prowadzonych obliczeń. Dostępne obecnie na rynku

komputerowe programy graficzne, mają z reguły wbudowane podprogramy

prowadzące analizę regresji i korelacji. Można tu wymienić takie pakiety programów jak Graphcr, Excel. SicmaPlot, itp.

2.3. METODY WERYFIKACJI

Oprócz omówionych metod estymacji oraz korelac ‘    ra-

cowywaniu wyników danych posługujemy się metodą weryfikacji hipotez statystycznych. Hipotezy' są pewnymi przypuszczeniami dotyczącymi wartości parametrów lub rozkładu badanej cechy w populacji generalnej. Pierwsza grupa

hipotez nosi nazwę parametrycznych, druga zaś nieparametrycznych. Wyróżnia się również hipotezy zerowa i alternatywne. Narzędziem do weryfikacji hipotez są testy statystyczne. Istota problemu przy budowie każdego testu polega na tym, aby uchronić się zarówno przed popełnieniem błędu pierwszego rodzaju, jak i błędu drugiego rodzaju. Błąd pierwszego rodzaju polega na odrzuceniu hipotezy' prawdziwej. Natomiast błąd drugiego rodzaju polega na przyjęciu hipotezy fałszywej. W praktycznych zastosowaniach najważniejsze znaczenie mają testy istotności. Hipotezę zerową i alternatywną możemy postawić tak, aby obszar krytyczny był lewostronny.