83264 skanuj0006

396

396

Mo,„

G,

Dla danych w rozważanym przykładzie: rezystancja jednostkowa

R_q = —= MO'³ {tym, R= -^g-10-³ = 2-10"²fl/m, Y-nr²    4*10“³

- indukcyjność jednostkowa ln- = 12*10"⁷H/m.

pojemność jednostkowa

= 9,3*10"¹²F/m,

ln-konduktancja jednostkowa

G₀ = C₀^- = 1,05 *10"¹⁰ S/m • ^fio

Współczynnik propagacji jest określony wzorem

y = a +jfi =    +j(x>L₀)(G₀ +/coCq) w

1₊

8ci)²l-^o C₀

W rozważanym przykładzie dla i?₀

= 2,78 *10"⁶ 1/m.

fi - <*JL₀C₀ Ostatecznie

8co²l-Ło

20,9-10"³1/m.

Y = a+jfi = (2,78 *10"®+ / 20,9 • 10"³) 1/m.

Impedancja falowa

Z, =

i?₀+;«L₀

\    c₀

i -

G,

2 co I Ln Cr

W rozważanym przykładzie można pominąć część urojoną impedancji

TT

Z,.

359 O.

Przykład 14.3

Należy wyznaczyć parametry L₀, C₀, impedancję falową Z_c, prędkość fazową v oraz długość fali X koncentrycznej, bezstratnej linii kablowej zasilanej ze źródła napięcia sinusoidalnego o częstotliwości / (rys. 14.3). Dane: r = 2mm, R = 6 mm, e_T = 2, /= 10 MHz.

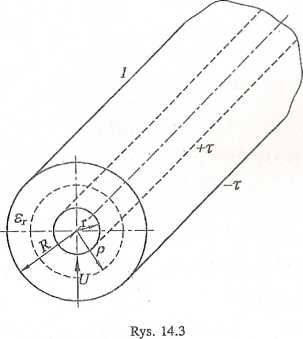
Rozwiązanie

Na podstawie prawa Gaussa

D‘ds = rl,

gdzie t - gęstość liniowa ładunku, stąd jy^ml = r/, więc £

27rQe_re₀

Napięcie między żyłą o promieniu r a płaszczem kabla o promieniu R

R    R

R

i 2ire_re₀e

dQ

2ir8„e_n

-ln^;

Pojemność na jednostkę długości linii kablowej <r 2ve_r8,