87582 skanuj0100 (21)

Tak więc dla (C₂H₅)₃PS, Z = 2 i M = 12, jednostka asymetryczna jest mniejsza niż jednostka formalna (C₂H₅)₃PS. Atomy S, P, i C (pomijając atomy wodoru trudniejsze do oznaczenia metodami rentgenograficznymi) znajdują się w położeniach szczególnych. Wystarczy podanie położenia jednego atomu P, jednego atomu S i atomów jednej grupy C₂H₅ do wyznaczenia położeń wszystkich innych atomów cząsteczki przez zastosowanie operacji symetrii.

W przypadku merocyjaniny (rys. 1.73) M = 4 i Z = 4[C₉H₁₁S₄N₃0]. Wszystkie atomy znajdują się w położeniach ogólnych. Ten ostatni przypadek dotyczy najczęściej struktury utworzonej przez zespoły cząsteczek o niskiej symetrii. W tych kryształach cząsteczkowych jednostka formalna pokrywa się z cząsteczką, a jednostka asymetryczna stanowi zwykle pojedynczą cząsteczkę, niekiedy połowę cząsteczki, rzadziej dwie cząsteczki.

Gdy zespoły atomów, cząsteczek lub jonów wieloatomowych zajmują położenia ogólne, ewentualna symetria tych zespołów nie pokrywa się z symetrią kryształu. Mówi się wówczas o symetrii niekrystalograjicznej. Przykładem może być symetria foremnego pięciokąta z rysunku 1.63. W cząsteczce merocyjaniny z rysunku 1.73 cząsteczki są płaskie¹ (w granicach błędów doświadczalnych), chociaż ich płaskość nie jest bynajmniej uwarunkowana grupą przestrzenną.

Symetria tego rodzaju nie ma nigdy charakteru jednoznacznego; możliwe odchylenia od symetrii doskonałej są związane z dokładnością wyznaczania położeń atomów. Przeciwnie, symetrię cząsteczkową pokrywającą się z symetrią krystalograficzną można w zasadzie ustalić w sposób jednoznaczny. Cząsteczki dimetyloformamidu w kompleksie NaI¹3DMF są dokładnie płaskie, ich płaszczyzna jest bowiem płaszczyzną zwierciadlaną kryształu (s. 98); gdyby jeden z atomów odsunął się nawet nieznacznie od płaszczyzny, jego obraz musiałby pojawić się po drugiej stronie płaszczyzny zwierciadlanej.

W badaniach nad strukturą kryształów szczególnie duże znaczenie mają odległości między atomami i kąty między wiązaniami łączącymi atom z dwoma atomami sąsiednimi.

Odległość R między dwoma atomami o współrzędnych x₁y₁z₁ i .x₂j>₂z₂ jest łatwa do obliczenia. Z zależności

Ax -    a(x₂)

Ay = b(y₂-yt)

Az =    c(z₂-)

otrzymuje się

R² = (Ax)² + (Ay)² + (Az)²+2AxAycosy+2AyAzcosa+2AxAzcos^

wyrażenia, w których a, b, c, a, /?, y są parametrami komórki elementarnej.

Kąt 6 między wektorami wiązania R_x i R₂ jest określony przez zależność między bo-

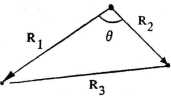
104

1

Z wyjątkiem CH₃ z grupy C₂H₅.