skanuj0142

mini odbity padał prostopadle na płytkę polaroidu. Teraz obracamy polaroid >v"kń| promienia odbitego, aż do uzyskania maksymalnego wyciemnienia pola widzenia. Następnie zmieniamy tak kąt padania a, aby odbity od próbki pro-iim ii był całkowicie wygaszany przez polaroid P.

Dla każdego dostarczonego materiału pomiar kąta 2ar powtarzamy kilka-Imiliiic. Ponieważ:

tg a- n (prawo Brewstera),

* I n wyższego wzoru możemy obliczyć współczynnik załamania n dostarczonych próbek.

/udanie 2

SI nawdzenie prawa Malusa.

I i/yjemy układu pomiarowego, którego schemat przedstawia iys.6.

.Aby sprawdzić prawo Malusa, ustawiamy polaryzator tak, aby dawał świa-ll" spolaryzowane w płaszczyźnie pionowej. Usuwamy filtr interferencyjny F₂ oi ii/ ówierćfalówki. Niech <p będzie kątem pomiędzy płaszczyznami drgań w ('"Irnyzatorze P\ i analizatorze P₂. Z prawa Malusa (7 =/₀ cos²(p) wynika, że •l|.i <p ^;:;0 zachodzi 7=7₀, natężenie światła przechodzącego przez analizator Ni największe. Takie ustawienie Pi i P₂, nazywamy równoległym. Jeżeli

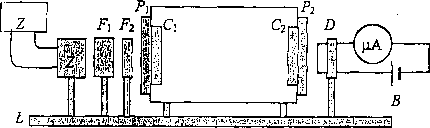
|i,. a. Schemat układu pomiarowego do obserwacji zjawiska polaryzacji: Ź - źródło światła z matówką i zasilaczem, F\ _ filtr wodny, F₂ - filtr interferencyjny (/ł=589nm), Pi - polaroid zwany polaryzatorem, P₂- Polaroid zwany analizatorem, D - fotoopór, pA - mikroamperomierz, B - źródło napięcia, C_t, C₂ -ćwierćfalówkij Ł - ława optyczna

płaszczyzny drgań polaryzatora i analizatora tworzą kąt 90°, wtedy I-0, a analizator całkowicie wygasza światło; takie położenie nazywa się skrzyżowanym.

W celu wykonania ćwiczenia ustawiamy analizator w położeniu równoległym i dobieramy tak zakres mikroamperomierza, aby wychylenie wskazówki przyrządu x (x - proporcjonalne do I) było bliskie maksymalnemu. Następnie ustawiamy P\ i P2 w położeniu skrzyżowanym i odczytujemy xo. Obracając analizator co 10°, odczytujemy wielkość x prądu w obwodzie fotooporu. Wyniki pomiarów ujmujemy w tabelę 1.

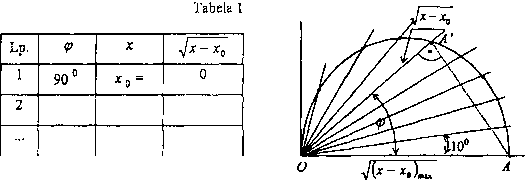
Rys.7. Przykład przedstawienia wyników pomiarów

Uzyskane wyniki przedstawiamy w układzie współrzędnych biegunowych: r, ę, gdzie na promieniu odkładamy ^x-x₀ (rys.7).

Wykres stanowi półokrąg zbudowany na ij(^x~^xo)_nm j^ak° średnicy. Z trójkąta O AA’ odczytujemy:

4^X~^Xo = /(^x~^xo)_m„^cosP i

zaś po podniesieniu obu stron do kwadratu:

(^x~^x o)⁼ (^x~^x o W cos V-

Ponieważ: (x~x ₀) ~ I, więc

/ = /„ cos² ę.