63460 MATEMATYKA060

112

m. Rachunek różniczkowy

x(2-Vx² —3x \

^l>'— vx>_+Sx-r-

,x + 2

1 — x

x_-2,

t+3

12

o) lim arclg-i—•,    ,_jm ^3ln*

**"    ^{2+x p} «.T®2+lnx’

DUinjK+arcsml), _s) i_{im (xc} «+2). t) lim 421

*-**•    *-•-«> J 3-x

q) lim

u) lim ln(2x-Vx^J-|), _v) lim 2arcsin-^, w) lim <4^)’’.

x—«■    1 -f- x*    “ ^v “

...    . 2 sinx_v

x⁾hm (x^J—j—■),

x-h» in x

7. Obliczyć granice:

x-*-« x -2

X

1

z) lim c

K >*•*

X'-!

.X Vx⁵+3-Vx+3    .... V5^7-2

a) nm y-    b) lim-7—,

^x_*° Vx‘+x+4-2    *-^kłx-V2-x

c) lim

x²-l

.v l-cos2x d) lim

e) limxctgx_ł

* ^i(x+lr 0 lim-^tgx.

x—»0 2x ’    x-*0    —    ' x-*0 X

8. Oblicz>'ć granice jednostronne funkcji f w punkcie x₀:

7 4- V    y * — 4

a) f(x) =    x_o = 0, b) f(x)=-_T — ’    x₀ = 2,

3x~x-    .x -4x + 4

I    l

c) f(x) = arcig--j,    x₀-l, d)f(x) = x + e^xt x₀=0.

^c)f(x) = ^. x₀ = l. g)f(x) = ie-^Ł‘, Xo = 0,

r\ _e. . l-2cosx

Of<X) =-7-5-, X₀ = 7l,

sin x

. _{v r/} . cosx ^{h f x) =} TTnx' *•'*’

i) f(x) = x + 2ⁿ"\ x₀ = e, j) f(x) = 3x+c⁴“^x2, x₀ = 2. 9. Oblicz>^rć granice:

a) hm(-+ctgx),    b) lim(ctgx-fln(-x)).

.0* x

1

c) lim(2-c^x'^,)»

X-*|4

X-»0-

1

d) lim xarctg _<> x-»2-    2 — X

*-*0 \‘

x 5

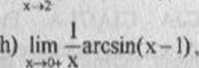
e) lim(—+c *^!),

g) lim (x²lnx-x),

O lim(3-c*’"^4x'⁴).

i) lim (3^X r'")₉

X * «! X

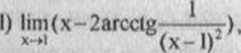
j) lim (arctg-_:-2arclgx).

k) lim(x-fln-~r),

x *o    X — 2

l) lim(xc

m) lim(ln(x-l)-f _T—).

x—>1*    1 — X

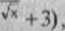
10 Wyznaczyć dziedzinę funkcji f i obliczyć jej granice w punktach brzegowych dziedziny, gdy

2

a) f(x) =

b) f(x) = xe ^

c) f(x) = xc^Vx,

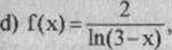
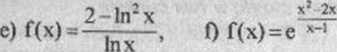
Odpowiedzi

3. a) 0,+»,0,-oc. b)+oo,-«*>,I.O.    4. a) +oc,l,+30,-ao, b) it,it/2,0, + ».

5. a)-l,-l,l,l, b)+oo,-4,4,-oo.

6 a) -oo, b) 1/2, c) O, d) -<*, e) -3/2, i) +oo, g)<>, h) 2/3. i) 5, j) -we. k) -oc, 1)0, 1)-oo, m)e^,u. n)c¹⁰, o)-x/4, p)3, q)4, r)-oo, s) +*, t)O, u) +oo, v)0, w) e\ x) 4-oc, y)0, z) I.

7. a)-2/>/3. b) -1/6, c) “OO, d)0, c) I, O

H a) f(0-)--oo, f((h)-+oc. b) f(2-)-f(2+)--oo, c) f(l-)«-x/2, f(1+)*ir/2, d) f(0-) = 0, l‘(0+)«+oo, e) f(l—)■ +oo, f(|+)«-*>, 1) f(Jt—)*f(jc+)■ +oo, g) f(0-)» -o©_f f(0+)«+oo, h) f(c-)«-oo, f(e-*)a foo, i) f(e-)= ■<-», f(c+)=-e.

j) f(2-)-6_ir(2-ł>j«+oo.

V. a) +oo, b) -oo, c) -oc, d) k. , e) +oo, f) 3, g) +«. h) -oo, i) -oo, j) Jt,

k)    -oo. 1) I. 1)3, m) -oo

10. a) D*(-»,0)u(2,+oo); 0,+oo,+oc,0, b)D«(I,+oo); (),+<*>, c)D«(-co,3)u(3,+oo) • os.+oo,O,+ oc, d) L)“(-oc^)u(2,3X O.+oo.-oo.O, e) l)-(0.1)vj(l,+*); +oo,-oo, +00,-00, O n=(-oc.lMI,+oo); 0,+oo.0,+oc