MATEMATYKA058

l()X

Ul. Rachunek różniczkowy

Inny sposób: Ponieważ sin x jest funkcją ograniczoną na zbiorze R

oraz lim — = 0. wiec z twierdzenia 1.3 wynika, żc lim -sinx = 0.

PRZYKŁAD 1.6 Obliczymy granice:

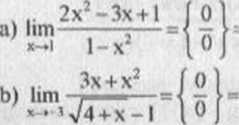
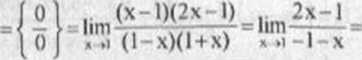
,    x(3+x)(>/4 + x + 1)

lim-=-

= lim x(v4+x + 1) = -6;

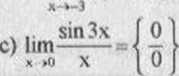
sin3x _<t    . . sint ,

—-— = {korzystamy 7 t\v. hm — = 1} - 3;

3x    not ’

PRZYKŁAD 1.7 Obliczymy granice

a) lim (2x + log_A(x+l)) = {+oo+ao} = +<»;

b) lim (x - In——) = {+«>- ln(0+)}={ +*>+*>} = +oo;

c) lim (e^ł*-e"^łx) = {e'*-c^,<c} = {o-oo} = ~ao;

d) lim (3— x)sin<arctgx) = < (—oo)sin-y l — { — oc-1} —o°.

PRZYKŁAD 1.8 Obliczmy granice jednostronne:

Licznik funkcji ma granicę równą 2, a mianownik dąży do 0. W takim przypadku trzeba określić znak mianownika odpowiednio w prawo- lub lewostronnym sąsiedztwie punktu x₀ = 2, aby można było skorzystać z

I .    1 _

twierdzeń, które zapisujemy umownie:    = +⁰⁰* q _ ⁼ 00 •

1 Otmiiea funkcji

Szkicujemy wykres mianownika; y=2x-x^? i odczytujemy; lim(2x-x²) = 0 i 2x-x^I<0 dla xeS*(2),

X .2.

co zapisujemy lim (2x~ x^:) -0-.

i-*2*

Analogicznie z wykresu odczytujemy, źc lim (2x - \²) 0+.

X »2

Zatem

,_imjLJLj 2 L_,    ,ń,±L.(iU;

* ^-2x-x* \ 0- j    *-*2-2x-x² 1 0+ J

b) lim    . lim

*-* i*x²+2x+1 1 0+■ /    x² +2x + l 1 0+ J

tel	• = +oo,	. 2-x J lim —— = 4	lir^1)
1 0- J		sin x I	l J

d) lim (^— +-_r^-) = |    +    l = {-cc-oo} = -co;

x Inx l-x [Ot 0-J

-00

c) lim (x-lnx) = { O-(-oc) } = +oo;

x-»0*

l	-1		— f ^1)
0 limę^1-* = X-»J+	n	’ ^= {^e } ^= 0t	lim e^,_x = -j>

g) lim (3”¹ - !n(-x)) = {3-!n(0+)} = {3+«} = -Mo;

x *0

h) lim xe *^: = jo-c °*j = {<) c"* }=0 0=0;

i) lim

cosx	[ cos2 ]	1 _ | cos2 |
ln(3-x)'	(ln(l+) j	1 «^+ 1

NIESKOŃCZENIE MAŁE. Na zakończenie rozważań o granicy funkcji wprowadzimy używane w' niektórych zagadnieniach |X>jęcic nieskończenie malej.

Funkcję f, określoną na pewnym sąsiedztwie punktu x₀, nazywamy nieskończenie małą przy x —> x₀, gdy lim f(x) = 0.

x