MATEMATYKA090

172 Ul. Rachunek różniczkowy

mają asymptoty ukośne (w szczególnym przypadku również poziomą)

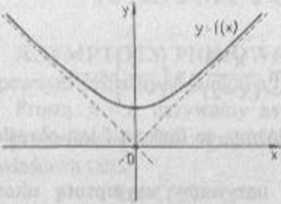
y

Rys 7.5    Rys 7.6

Zauważmy, żc krzywa może mieć inną asymptotę w plus nieskończoności, a inną - w minus nieskończoności

W pewnych przypadkach możemy łatwo znaleźć asymptoty ukośne wykresu funkcji, korzystając jedynie z podanych wyżej definicji Na przykład:

a) Prosta y = 2x + l jest asymptotą ukośną wykresu funkcji f(x) =    + 2x +1 w płus nieskończoności, gdyż

lim (f(x)-2x-l)= lim = 0;

x-*‘Oj    * >-<o in x

b) Ponieważ

lim

3-2Inx

^:-2,

* »*«o l + lnx

więc prosta y = -2 jest asymptotą poziomą krzywej y

ln x

l + lnx

w plus

nieskończoności (krócej przy x-> -ł<r).

Przy wyznaczaniu asymptot ukośnych korzystamy z niżej podanego twierdzenia, które stanowi warunek konieczny i wystarczający istnienia asymptoty ukośnej

TWIERDZENIE 7.1 Prosta o równaniu y = mx + n jest asym-ptolą ukośną krzywej y = f(x) przy x-M<*> (przy x-*-«>) wicdy i t>'lko wtedy, gdy

m= lim    i n= lim (f(x)-mx).

x-m<© X

(X-*-«>    (x~* «)

Uwaga Jeżeli prznajmniej jedna z tych granic me istnieje lub jest niewłaściwa, to asymptota ukośna nic istnieje

PRZYKŁAD 7.) Znajdziemy asymptoty krzywej y = f(x), gdy

i

X

a) f(x)

b) f(x) = xc

ln(x-3) *

a) Dziedziną funkcji f jest zbiór D = (3,4)vj(4,+oo). Najpierw znajdziemy, o ile istnieją, asymptoty pionowe danej krzywej Zauważmy, żc jedynymi punktami, w których mogą istnieć granice jednostronne niewłaściwe funkcji f są punkty x = 3 i x = 4 Obliczamy:

lim r~r ln(x

lim

% »♦- ln(x

L_JJ_

-3) \-oo -3) \0-

= 0,

= -oc,

lim r~r x-^4*ln(x

-3) ⁼ {o₊} ⁼

+00.

Stąd wynika, żc rozpatrywana tu krzywa ma tylko jedną asvmplotę pionową: x = 4.

Ponieważ funkcja f nie jest określona w sąsiedztwie -co, więc asymptoty ukośnej należy szukać jedynie przy' x —» +oo. Zgodnie z twierdzeniem 7.1 obliczamy:

= 0=m,

lim = lim - . ■ -,-r

lim (f(x)-mx)= lim , /-.t = lim —7— - lim (x-3) = +oo. _K^«ln(x-3) 11 k-+ioc I

x-3

Ponieważ jedna z tych granic jest niewłaściwa, asymptota ukośna nic istnieje

Jedyną asymptotą krzywej y = f(x) jest asymptota pionowa

x = 4.

b) Dziedziną funkcji fjest zbiór D = (-00,0) u (O, +00). Jedynym punktem, w którym funkcja może mieć granice jednostronne jest punkt x = 0. Obliczamy:

lim xc * = {0c"} = 00=0,

x-»0*    *