MATEMATYKA100

190 Ul. Rachunek różniczkowy

Rys 8 6    Rys 8.7

ZADANIA DO ROZWIĄZANIA.

1. Zbadać przebieg zmienności i naszkicować wykres funkcji y = y(x)

a) y = 6x²-8x³+3x⁴, b) y =

lnx

^d)y⁼—’

c)y=-^e'.

c) y=

0 y =

x—1 xVx ’ c^x

g) y = xe², ł) y = x-2arctgx,

h) y = x²lnx, I x

k) y = In

m) y =

x-2 ’

ln|x| *

(x + l)² ’ i) y=x²|lnx|, l)y=ln(x³-3x + 2),

n) y = ln(x + /x² +1)

2.

Zbadać przebieg zmienności i naszkicować wykres funkcji y = y(x) a) y = (x- l)⁴(x+2), b) y = (x + 2)³(x-1), c) y = xc

..    x⁵-4

d) y = —jr

_%    x^z+2x-6    „ r;

c)y=-:—,    0y=c*²,

g)y = ~4-2arctgx. j) y = x>/2-lnx,

I)y=

Vlnx-1 ’

h) y = ln'x+31n^?x,    i)y = xe^_l/*\

k) y=21n(lnx)-lnx, I) y = x²c"³\

i

_m) y=c^x>+2xJ,    n) y = x²ln(-x),

o)y = x + |-2lnx. p) y=arcsin-j^_r, r)y^arctg~j,

2x    1    1

s) y=arcsin--- - 2arctgx, t) y = arcsui ... ■■ - arctg-,

l + x²    Vl+x²    *

u) y = 2+Vl-x² +Vx^:-1,    w) y = l+Vćósx-l+ln(3-|2-x|).

3. Zbadać krzywą określoną równaniami parametrycznymi x = cos³1, y = sin^Jt, teR.

Odpowiedzi.

1. Niżej podajemy tabele ilustrujące przebieg zmienności badanych funkcji. Naszkicowanie wykresów pozostawiamy Czytelnikowi

a) 1>R, y' * 12x(x-1)², y" = 12(3x-lXx-1).

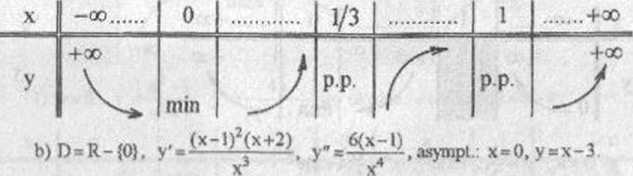
X	-00......	-2		0		1	.......+00
y	-00	max	~\ -00		r 3 -00	PP	+oc

c) L)b(0,+0O),    y'.-2liL,

2 x²Vx    4xwx

X	0		3		5	......+00
y	IIP • f< > <■* ❖	-00	max	'N	PP	V^0