60082 MATEMATYKA055

102 Ul Rachunek różniczkowy

DEFINICJA CAUCHY EGO

(lim f(x) = g) o A V A(x>K=s>|f(x) -g|<e).

* »**.    c>0 K x

Analogicznie, gdy funkcja jest określona na pewnym sąsiedztwie punktu niewłaściwego -oo, można rozważać istnienie granicy właściwej lub niewłaściwej tej funkcji przy' x -> -co.

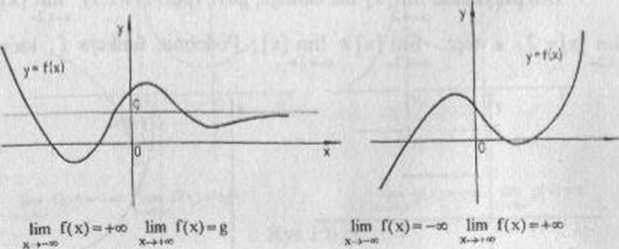
Rys 1.9    Rys MO

PRZYKŁAD 1.3 Na rysunkach 19 - 1.11 przedstawione są różne przypadki istnienia granicy funkcji przy' x -> -oo oraz przy _x_>+co. Z rysunku 1.11 odczytujemy granice funkcji wykładniczej

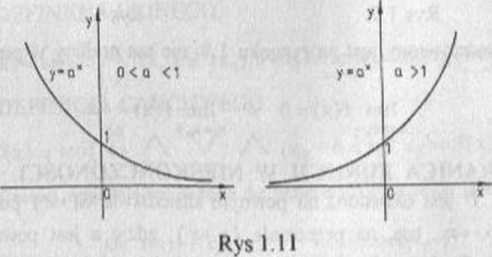
w plus i minus nieskończoności:

0<a<l =>(lima*=+XA lim a* = 0)

x »-*«    X »♦*>

oraz

a>l =>(lima^x=0A lim a* - -foo).

X-»-Q»    X

lim 4)’ = +x, lim 3” = 0,    lim(|)' = 0    ■

Zatem

X »-«• Z    X-* *    X kt>V J

PRZYKŁAD 1.4 Korzystając z definicji Heinego obliczymy

granice:

a) lim

3 + x^J

* * 2 + x

3 i x^;

_a) Funkcja f(x) = --jest określona dla x e D = (-oo,-2)u

Niech (x_n) będzie dowolnym ciągiem takim, że _{v 6}S(-^a0)^c:^» neN oraz x_n >-x. Obliczamy granicy ciągu

(f(Xn))^:

\ I    ^{3 + X}

limf(x_n)-lmi-

_tl MO    "    ~ ^X

f.j	r«o	— + K 1 - lim ^X"
.	1 ~^x 1	n™ 2 .
	L i	— + 1
		^Xn

-oo

= -X.

Zatem zgodnie z definicją Heinego granicy funkcji

..    3-f x

lim -— = -x.

x—«- »> 2 + x

b) Funkcja f(x) = (1 +-)* jest określona dla x c- D - (-oo, 1)^

X

u(0,+x) Niech (x„) będzie dowolnym ciągiem takim, że x„ e S( h<») c D oraz x_n +x. Obliczamy granicę ciągu (f(x_D))

lim f(x_B) = lim(l + — )*• - e

Zatem

lim (1 + —)* =c,

X-*oo X

1

Analogicznie otrzymujemy:

(lim f(x) = ±oo) => (lim (1 +-jtt-t)^{1 łl} = c)

X *X₀    X >X₀ I V^x /